Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze
Nun müssen wir noch überprüfen, ob das ermittelte Ergebnis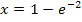 
überhaupt innerhalb der Definitionsmenge 
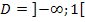liegt. Man kann sofort erkennen, dass 
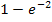sicher kleiner ist als 1 und damit in der Definitionsmenge liegt.
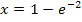ist also wirklich Lösung der Gleichung.
(Du kannst 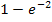natürlich auch in den Taschenrechner eingeben;dann erhältst du das Ergebnis 
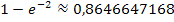und das ist offensichtlich kleiner als 1.)
Woran lässt sich aber direkt erkennen, dass 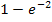sicher kleiner ist als 1, ohne den Ausdruck mit dem Taschenrechner auszurechnen?
Bekanntlich ist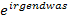 
grundsätzlich positiv und somit ist auch 
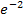sicher positiv. (Dass 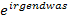immer positiv ist, erkennt man am Graph der e-Funktion 
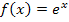;er verläuft immer oberhalb der x-Achse. Siehe auch: Das Wichtigste zur e-Funktion) Der Ausdruck 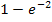bedeutet, dass von der Zahl 1 die positive Zahl 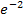abgezogen werden soll. Wenn von 1 etwas abgezogen wird, ergibt sich natürlich eine Zahl, die kleiner ist als 1. Deshalb ist 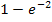sicher kleiner als 1 und liegt in der Definitionsmenge .
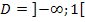Zu 4c.)
Hier noch einmal die Angabe: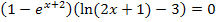 
1. Definitionsmenge ermitteln:
Bei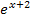 
kann man jede beliebige reelle Zahl für x einsetzen;dabei gibt es also keine Schwierigkeit. (Die e-Funktion 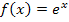ist schließlich für x 
ℝ definiert. Siehe auch: Das Wichtigste zur e-Funktion)
Bei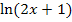 
muss das Argument 
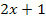allerdings positiv sein, damit der ln überhaupt definiert ist. (Logarithmen sind grundsätzlich nur für positive Argumente definiert. So ist z.B. lnx nur für x >0 definiert.) Es ist daher folgende Ungleichung zu lösen:
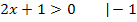
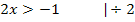
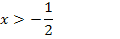
Die Definitionsmenge lautet somit: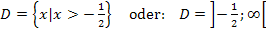 
2. Gleichung lösen
Hier noch einmal die Angabe: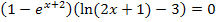
Diese Gleichung mag dir zuerst schwierig vorkommen, doch im Prinzip ist sie es gar nicht. Es handelt sich nämlich um eine Gleichung der Form „Produkt gleich Null“ und solche Gleichungen lassen sich lösen, indem man jeden Faktor des Produkts einzeln gleich Null setzt und jeweils nach x auflöst. Also keinesfalls die Klammern ausmultiplizieren;das würde es erst richtig schwierig machen!
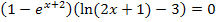
Die Faktoren des Produkts einzeln gleich Null setzen und jeweils nach x auflösen
Nun müssen wir noch überprüfen, ob die berechneten Werte überhaupt in der Definitionsmenge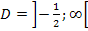 
liegen.
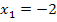liegt offensichtlich nicht in 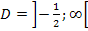und ist somit keine Lösung der Gleichung.
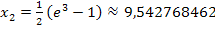liegt dagegen schon in 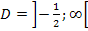. Daher lautet die einzige Lösung der Gleichung: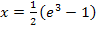 
Zu 4d.)
Hier noch einmal die Gleichung: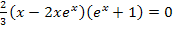 
Die Definitionsmenge ist hier nicht gefragt;sie ist sowieso D = ℝ.
