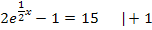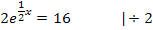Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze

Definitionsmenge von 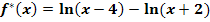ermitteln:

Das Argument x - 4 des ersten ln muss positiv sein und das Argument x + 2 des zweiten ln muss positiv sein. Beide Argumente des ln müssen demnach zugleich positiv sein. Es muss gelten:

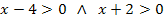
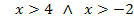
Das entspricht genau dem 1. Fall, den wir bei der anderen Funktion bereits besprochen haben. Siehe oben! Daher gilt:

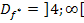
Wo ist denn nun aber der andere Bereich 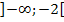geblieben? In diesem Bereich ist 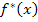nicht definiert, weil die Argumente x – 4 und x + 2 dann negativ würden und dann wäre der ln nicht definiert.

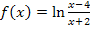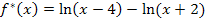Man erkennt, dass die Funktionen und offensichtlich nicht die gleichen Definitionsmengen besitzen!

Daher darf man die Funktion 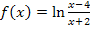nicht einfach mit dem zweiten ln-Rechengesetz zu 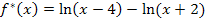umformen.

Anders wäre es bei der Funktion 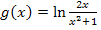. Durch Verwendung des zweiten ln-Rechengesetzes ergibt sich:

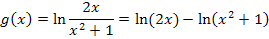
Durch diese Umformung ändert sich die Definitionsmenge nicht. Es können jeweils nur positive Zahlen für x eingesetzt werden: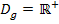

Erläuterung:

Die Funktion 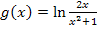ist nur definiert, wenn der Bruch größer Null ist. Der Nenner ist hier sowieso immer positiv, da 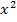wegen der geraden Potenz nicht negativ sein kann und somit 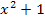sicher positiv ist. Damit der Bruch positiv ist, muss also auch der Zähler 2x positiv sein. Das ist der Fall, wenn x selbst ebenfalls positiv ist. Daraus folgt: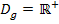

Die Funktion 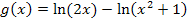ist nur dann definiert, wenn die beiden Argumente 2x und 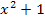positiv sind. 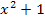ist wegen der geraden Potenz von x immer positiv, egal was man für x einsetzt. 2x ist positiv, wenn x positiv ist. Daraus folgt: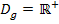

Es gilt also für 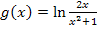und 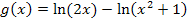die gleiche Definitionsmenge. Das ln-Rechengesetz darf ohne Einschränkung angewendet werden.

Ausführlichere Erklärungen zum Thema Definitionsmenge von ln-Funktionen findest du bei:

Definitionsmenge ermitteln bei e- und ln- Funktionen

Jetzt wollen wir aber endlich ein paar Aufgabenbeispiele anschauen, wo man den ln braucht bzw. in denen der ln vorkommt.

4. Bsp.:Gleichungen mit e und ln

Löse die folgenden Gleichungen! Gib bei den Teilaufgaben 4b., 4c. und 4g. auch die Definitionsmenge an!

a.)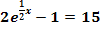

b.)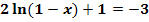

c.)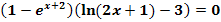

d.)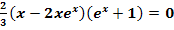

e.)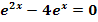

f.)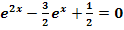

g.)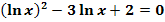

Lösung:

Zu 4a.)

Hier noch einmal die Angabe: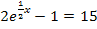

Diese Gleichung ist nicht schwer zu lösen. Wir müssen die Gleichung nur so umstellen, dass 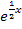alleine auf einer Seite der Gleichung zu stehen kommt. Dann kann man den ln anwenden, um den Exponenten 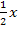herunter zu holen.

1. Schritt:Nach 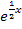umstellen

---