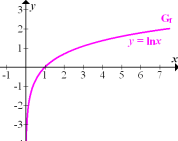
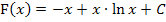Die ln-Funktion:y = lnx
Zur Erinnerung hier noch einmal die Produktregel in Worten:
1. Faktor ableiten mal 2. Faktor hinschreiben + 1. Faktor hinschreiben mal 2. Faktorableiten
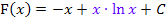
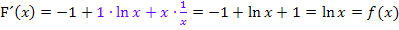
Damit ist nachgewiesen, dass 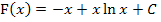 tatsächlich Stammfunktion zu
tatsächlich Stammfunktion zu 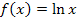 ist.
ist.
Für interessierte Schüler:Im Kapitel „Einführung in die Integralrechnung“ Abschnitt Weitere Integrationsregeln wird im Anschluss an den G8- Stoff auch noch erklärt, wie die Integration der ln-Funktion gelingt, wie man also überhaupt auf die Stammfunktion F der ln-Funktion kommt. Das Verfahren nennt sich „partielle Integration Typ Faktor 1“. Es steht jedoch nicht auf dem Lehrplan für Gymnasien in Bayern.
Wir fassen zum Abschluss dieses Teils noch einmal das Wichtigste zur Funktion 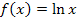 übersichtlich zusammen:
übersichtlich zusammen:
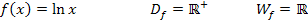
Wichtig:
Graph Stammfunktion zu
|
- Page 4 of 4
- « Previous
- 1
- 2
- 3
- 4
- Next »

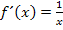

 streng monoton steigend
streng monoton steigend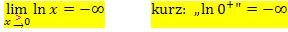
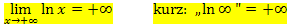
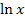 wächst langsamer als jede Potenz- oder Polynomfunktion und natürlich auch langsamer als
wächst langsamer als jede Potenz- oder Polynomfunktion und natürlich auch langsamer als 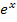 !
!