Die ln-Funktion:y = lnx
Dass es keinen Schnittpunkt der ln-Funktion mit der y-Achse gibt, merkt man auch, wenn man versucht seine Koordinaten zu berechnen. Jeder Punkt der y-Achse hat bekanntlich die x-Koordinate x = 0. Daher muss man für x die Zahl 0 in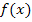 
einsetzen, also 
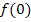bilden, wenn man die y-Koordinate eines Schnittpunkts mit der y-Achse berechnen will. Wegen 
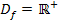ist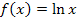 
an der Stelle x = 0 aber gar nicht definiert, so dass man 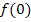überhaupt nicht bilden kann. Einfacher gesagt:„ln0“ gibt´s gar nicht! (Das darf man eigentlich gar nicht hinschreiben, daher hier die Schreibweise mit den Anführungszeichen. Du schreibst selbst aber wirklich niemals „ln0“ außer im Zusammenhang mit einem Grenzwert, dazu aber gleich noch mehr.) Daraus folgt:Die Funktion 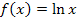schneidet die y-Achse nicht!
Nullstelle der ln-Funktion, Schnittpunkt mit der x-Achse:
Der Graph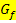 
der ln- Funktion schneidet die x-Achse offensichtlich im Punkt N(1|0) und hat somit die Nullstelle x = 1. (Vergleiche Abbildung oben!)
Dies folgt auch daraus, dass die e-Funktion die y-Achse im Punkt (0|1) schneidet, wegen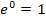 
. Du weißt:Einer Spiegelung an der Winkelhalbierenden y = x entspricht rechnerisch das Vertauschen von x- und y-Koordinate der Kurvenpunkte. Wenn also der Punkt (0|1) auf der e-Funktion liegt, muss demnach der Punkt (1|0) auf der ln-Funktion liegen. Deshalb gilt:
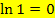
Man könnte das auch durch Rechnung herleiten:
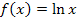
Nst.: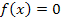 
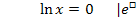
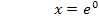
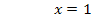
Die ln-Funktion schneidet die x-Achse folglich im Punkt N(1|0).
Verhalten der ln-Funktion an den Rändern der Definitionsmenge:
Die Definitionsmenge der ln-Funktion lautet: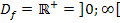 
Die Ränder der Definitionsmenge sind jeweils die kleinste und größte Zahl, die man gerade nicht mehr einsetzen kann und eventuell vorhandene Definitionslücken. Weil es bei 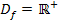keine Lücken gibt, müssen nur die Stellen x = 0 (linker Rand) und 
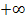(rechter Rand) untersucht werden.
An die Stelle x = 0 können wir uns nur von der rechten Seite her annähern, da die ln-Funktion schließlich nur für positive x-Werte definiert ist.
Wir müssen also folgende Grenzwerte ermitteln: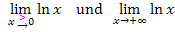 
Dazu betrachtest du am besten noch einmal den Graph der ln-Funktion. (Siehe Abb. oben!)
Überlege dir nun zuerst den Grenzwert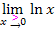 
. Nähere dich also in Gedanken immer mehr von rechts an die y-Achse x = 0 an und schau, wohin der Graph 
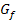geht. Was passiert mit den y-Koordinaten der Kurvenpunkte von 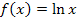, wenn man ganz nah an die y-Achse heran geht?
Richtig!
