Die ln-Funktion:y = lnx
Die natürliche Logarithmus-Funktion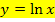 
und die natürliche Exponentialfunktion 
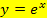sind zueinander Umkehrfunktionen. Das bedeutet, dass sich der Graph der einen Funktion durch Spiegelung des anderen Graphen an der steigenden Winkelhalbierenden y = x ergibt. So ergibt sich der Graph der ln-Funktion durch Spiegelung des Graphen der e-Funktion an y = x und umgekehrt der Graph der e-Funktion durch Spiegelung des Graphen der ln-Funktion an y = x.
Welche der beiden Funktionen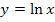 
und 
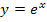dabei als Funktion 
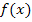und welche als Umkehrfunktion 
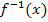betrachtet wird, kann man nicht konkret sagen. Wenn man festlegt, dass gilt 
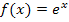, dann ist deren Umkehrfunktion 
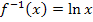. Umgekehrt kann man natürlich auch von 
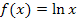ausgehen und dann 
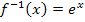als Umkehrfunktion auffassen. Genau davon werden wir im Folgenden ausgehen. Wir verwenden ab sofort die Bezeichnungen:
Der Verlauf des Graphen der e-Funktion, sowie Definitions- und Wertemenge der e-Funktion 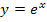werden als bekannt vorausgesetzt. (Näheres dazu bei:Das Wichtigste zur e-Funktion)
Zur Erinnerung:
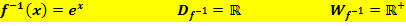
Bei der e-Funktion darf man für x alle reellen Zahlen (auch negative Zahlen oder Null) einsetzen, aber es können bei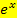 
ausschließlich positive Zahlen herauskommen 
.
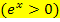Genau umgekehrt muss es dann bei der ln-Funktion sein. Du weißt hoffentlich:Definitions- und Wertemenge sind bei Umkehrfunktionen jeweils genau vertauscht.
Es gilt: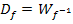 
und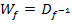 
Demnach ergibt sich für die Definitions- und Wertemenge der ln-Funktion:
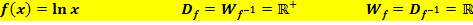
Bei lnx darf man nur positive Zahlen einsetzen, aber es kann jede beliebige reelle Zahl herauskommen. In anderen Worten:Der natürliche Logarithmus lnx ist (wie auch alle anderen Logarithmen) ausschließlich für positive Argumente x definiert. Lnx kann aber positive oder negative Werte ergeben und sogar gleich Null sein.
Graph der ln-Funktion:
Wie oben schon erwähnt, ergibt sich der Graph der ln-Funktion durch Spiegelung des Graphen der e-Funktion an der Winkelhalbierenden des I. und III. Quadranten, also an der Geraden y = x.
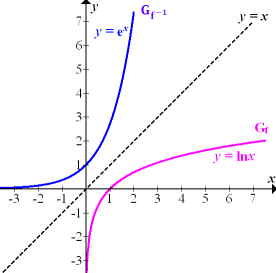
Abb.:Der Graph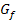 
der ln- Funktion entsteht durch Spiegelung des Graphen 
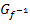der e-Funktion an der Winkelhalbierenden des I. und III. Quadranten y = x.
Weil die ln-Funktion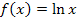 
bloßfür positive Werte definiert ist, verläuft ihr Graph nur rechts von der y-Achse. Da 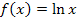jedoch beliebige reelle Funktionswerte (d.h. y-Werte) annehmen kann, verläuft ihr Graph sowohl unterhalb als auch oberhalb der x-Achse und schneidet die x-Achse auch. Der Graph von 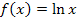verläuft somit ausschließlich im I. und IV. Quadranten. Vergleiche Abb.!
Schnittpunkt mit der y-Achse:
Die ln-Funktion schneidet die y-Achse niemals;ihr Graph schmiegt sich zwar beliebig nah an die y-Achse an, berührt oder schneidet sie aber nicht, obwohl das in der Abbildung oben vielleicht so wirken könnte! (Die y-Achse ist die senkrechte Asymptote von 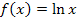und der Graph schneidet seine senkrechte Asymptote grundsätzlich nicht.) Weil die e-Funktion für x gegen 
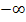die x-Achse als waagrechte Asymptote besitzt, muss entsprechend bei der ln-Funktion die y-Achse senkrechte Asymptote sein.
