Die ln-Funktion spiegeln, stauchen/strecken und verschieben
Die Funktion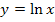 
ist bekanntlich streng monoton steigend. Weil der Graph von 
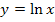durch Spiegelung an der y-Achse aus dem Graph von hervorgeht, muss 
zwangsläufig streng monoton fallend sein. Nur der rosafarbene Graph erfüllt diese Bedingungen;er gehört zur Funktion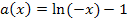 
.
Der Graph 
der Funktion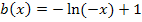 
ergibt sich aus dem Graphen von 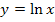durch Spiegelung an der x- und y-Achse mit nachfolgender Verschiebung um 1 nach oben. Die Funktion 
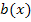ist nur für negative x definiert;ihr Graph verläuft somit genauso wie der rosafarbene Graph 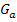ausschließlich links von der y-Achse. Die Funktion 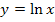ist bekanntlich streng monoton steigend. Weil der Graph von 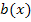durch Spiegelung an der x- und y-Achse aus dem Graph von 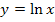hervorgeht, muss zwangsläufig auch streng monoton steigend sein. Nur der hellblaue Graph erfüllt diese Bedingungen;er gehört zur Funktion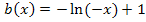 
.
Die Funktion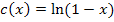 
ist ausschließlich für Zahlen unter 1 definiert, weil das Argument des ln immer positiv sein muss. Der Ausdruck 1 – x muss also größer als Null sein;dies ist nur für x <1 der Fall. Bei x = 1 hat die Funktion eine senkrechte Asymptote. Der Graph 
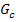verläuft wegen 
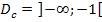immer links von der senkrechten Asymptoten x = 1. Nur der blaue Graph kommt daher in Frage. Der dunkelblaue Graph gehört zu .
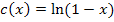Der Graph 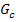entsteht übrigens durch Verschiebung des Graphen von 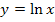um 1 nach links und anschließender Spiegelung an der y-Achse. Alternativ dazu kann man den Graph von 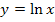auch zuerst an der y-Achse spiegeln und nachher um 1 nach rechts verschieben, um den Graph 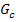zu erzeugen. Das wird allerdings erst dann klar, wenn man die Funktion 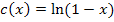vorher folgendermaßen umformt:
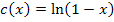
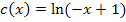
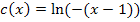
Der Graph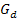 
der Funktion 
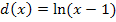entsteht aus dem Graphen von 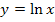durch Verschiebung um 1 nach rechts. Die Funktion 
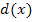ist nur für x >1definiert;ihr Graph verläuft somit ausschließlich rechts von ihrer senkrechten Asymptote x = 1. Nur der rote Graph erfüllt diese Bedingungen;er gehört zur Funktion .
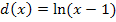Für die Funktion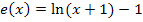 
bleibt jetzt bloßnoch der grüne Graph übrig. Dass der grüne Graph wirklich zu 
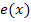gehört, erkennt man unter anderem an der Definitionsmenge von 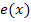. Der ln ist nur dann definiert, wenn sein Argument, also hier der Ausdruck x + 1, positiv ist. Die Ungleichung x + 1 >0 ist ausschließlich für x >-1 erfüllt. Die Funktion 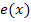ist daher ausschließlich für x >-1 definiert und hat bei x = -1 eine senkrechte Asymptote. Der Graph 
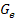entsteht aus dem Graph von 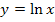durch Verschiebung um 1 nach links und um 1 nach unten. Der grüne Graph passt tatsächlich zur Funktion 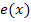, er ist auch der einzige der dargestellten Graphen, der bei x = -1 eine senkrechte Asymptote aufweist.
