Die ln-Funktion spiegeln, stauchen/strecken und verschieben
Abschließend noch ein kleiner Tipp zu ln-Funktionen mit Betrag um den gesamten Funktionsterm herum:
Den Graph einer Funktion der Form 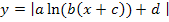 erhältst du, indem du nur den unterhalb der x-Achse liegenden Teil des Graphen der Funktion
erhältst du, indem du nur den unterhalb der x-Achse liegenden Teil des Graphen der Funktion 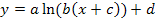 an der x-Achse nach oben spiegelst. Am oberhalb der x-Achse liegenden Teil des Graphen von
an der x-Achse nach oben spiegelst. Am oberhalb der x-Achse liegenden Teil des Graphen von 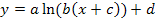 änderst du gar nichts. Es entsteht dadurch am Graph der für Betragsfunktionen typische „Knick“ an der Nullstelle. Schauen wir uns dafür gleich ein konkretes Beispiel an.
änderst du gar nichts. Es entsteht dadurch am Graph der für Betragsfunktionen typische „Knick“ an der Nullstelle. Schauen wir uns dafür gleich ein konkretes Beispiel an.
5. Bsp.:
Es soll der Graph 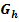 der Funktion
der Funktion 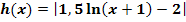 schrittweise aus dem Graph
schrittweise aus dem Graph 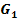 der Funktion
der Funktion 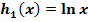 hergeleitet werden. Zeichne dazu die Graphen der folgenden Funktionen:
hergeleitet werden. Zeichne dazu die Graphen der folgenden Funktionen:
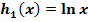
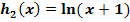
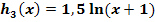
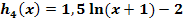
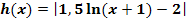
Welche Abbildung muss durchgeführt werden, um aus dem Graph 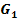 der Funktion
der Funktion 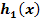 den Graph
den Graph 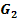 der Funktion
der Funktion 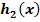 herzuleiten, welche um vom Graph
herzuleiten, welche um vom Graph 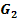 der Funktion
der Funktion 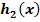 zum Graph
zum Graph 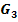 der Funktion
der Funktion 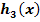 zu kommen usw. bis zum Graph
zu kommen usw. bis zum Graph 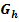 der Funktion
der Funktion 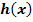 ?
?
Lösung:
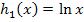
Verschiebung von links ergibt |
 |
|||
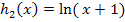
Streckung von y-Achse mit dem Faktor 1,5 ergibt |
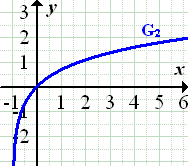 |
|||
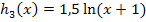
Verschiebung von unten ergibt |
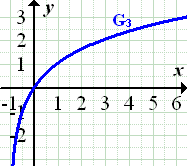 |
|||
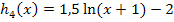
Spiegelung des unterhalb der x-Achse liegenden Teils von an der x-Achse ergibt |
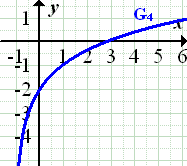 |
|||
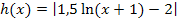 |
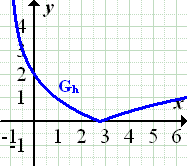 |
Sehr häufig finden sich in Prüfungen auch Aufgaben, bei denen du einigen gegebenen Graphen den jeweils zugehörigen Funktionsterm zuordnen musst. Im nächsten Beispiel kannst du so eine Aufgabe sehen.
6. Bsp.:Graphen zuordnen
Gegeben sind die Funktionen:
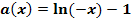
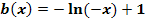
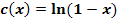
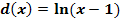
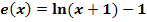
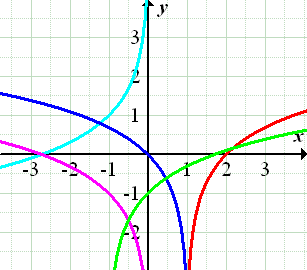
In der nachfolgenden Abbildung sind die Graphen dieser Funktionen dargestellt. Welcher Graph gehört zu welcher Funktion?
Lösung:
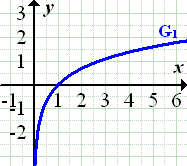
Die angegebenen Funktionen lassen sich mit Hilfe ihrer Definitionsmenge und ihres Monotonieverhaltens bzw. des Verhaltens in der Umgebung der senkrechten Asymptote den in der Abbildung dargestellten Graphen zuordnen. Du kannst dir aber auch überlegen durch welche Abbildungen der Graph der jeweiligen Funktion aus dem Graphen von 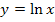 entsteht. Dadurch kann man sich den Verlauf des zugehörigen Graphen grob vorstellen und ihn richtig zuordnen.
entsteht. Dadurch kann man sich den Verlauf des zugehörigen Graphen grob vorstellen und ihn richtig zuordnen.
Rosa 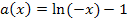
Hellblau 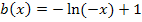
Dunkelblau 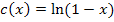
Rot 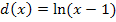
Grün 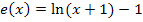
Erläuterungen:
Der Graph 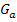 der Funktion
der Funktion 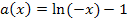 entsteht aus dem Graphen von
entsteht aus dem Graphen von 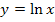 durch Spiegelung an der y-Achse und anschließender Verschiebung um 1 nach unten. Die Funktion
durch Spiegelung an der y-Achse und anschließender Verschiebung um 1 nach unten. Die Funktion 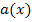 ist nur für negative x definiert;ihr Graph verläuft somit ausschließlich links von der y-Achse.
ist nur für negative x definiert;ihr Graph verläuft somit ausschließlich links von der y-Achse.

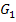 um 1 nach
um 1 nach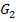 .
.
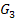 .
.
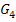 .
.
 .
.