Die ln-Funktion spiegeln, stauchen/strecken und verschieben
Die Funktion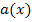 
steht bereits in der Form 
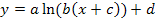da. Man kann also direkt ablesen:
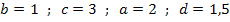
Der Graph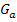 
der Funktion 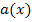entsteht deshalb durch folgende Abbildungen aus dem Graph 
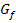der Funktion 
:
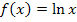- Keine Spiegelung an der y-Achse (weil b positiv ist) und keine Stauchung/Streckung entlang der x-Achse, wegen b = 1
- Verschiebung um 3 nach links (weil c positiv ist)
- Keine Spiegelung an der x-Achse (weil a positiv ist)
- Streckung mit dem Faktor 2 entlang der y-Achse, wegen
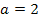
- Verschiebung um 1,5 nach oben (weil d positiv ist)
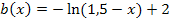
Im Argument des ln, also innerhalb der Klammer hinter dem ln, muss zuerst die Reihenfolge vertauscht und das Minus ausgeklammert werden, um die Funktion auf die Form 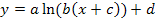zu bringen:
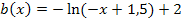
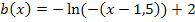
Jetzt kann man ablesen:
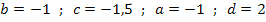
Der Graph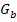 
der Funktion 
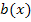entsteht deshalb durch folgende Abbildungen aus dem Graph 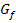der Funktion :
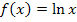- Spiegelung an der y-Achse, aber keine Streckung/Stauchung entlang der x-Achse, wegen
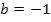
- Verschiebung um 1,5 nach rechts (weil c negativ ist)
- Spiegelung an der x-Achse, aber keine Streckung/Stauchung entlang der y-Achse, wegen
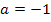
- Verschiebung um 2 nach oben (weil d positiv ist)
Alternativ zur soeben beschriebenen Vorgehensweise kannst du auch folgendermaßen vorgehen:
Das Minuszeichen innerhalb der Klammer hinter dem ln wird vorweg nicht ausgeklammert;es wird also von der folgenden Form der Funktion ausgegangen:
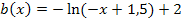
Nun überlegt man sich die Abbildungen von innen nach außen.
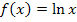
Verschiebung von um 1,5 nach links
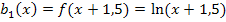
Spiegelung von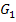 
an der y-Achse
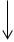
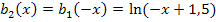
Spiegelung von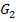 
an der x-Achse
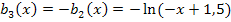
Verschiebung von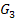 
um 2 nach oben
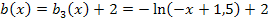
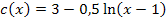
Die Funktion steht schon fast in der Form 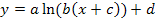da. Am besten erkennst du die Koeffizienten a, b, c und d, wenn du die Reihenfolge im Term von 
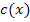etwas veränderst. Man kann die Funktion schließlich auch in der folgenden Form schreiben:
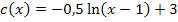
So lässt sich leicht ablesen:
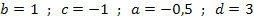
Der Graph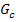 
der Funktion 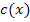entsteht also durch folgende Abbildungen aus dem Graph 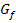der Funktion :
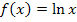- Keine Spiegelung an der y-Achse und keine Streckung/Stauchung entlang der x-Achse, wegen
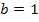
- Verschiebung um 1 nach rechts (weil c negativ ist)
- Spiegelung an der x-Achse (weil a negativ ist)
- Stauchung entlang der y-Achse mit dem Faktor 0,5
- Verschiebung um 3 nach oben (weil d positiv ist)
Man kann alternativ dazu natürlich auch wieder „von innen nach außen“ vorgehen.
