Die ln-Funktion spiegeln, stauchen/strecken und verschieben
Zum Schluss wird der Graph um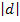 
nach oben bzw. unten verschoben. Bei d ist die Richtung des Verschiebens so, wie man es auch aus dem Bauch heraus machen würde:Bei positivem d verschiebt man nach oben und bei negativem d nach unten.
Bei der Verschiebung um 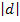nach oben/unten kannst du also – anders als bei c – ruhig so vorgehen, wie du es wegen des Vorzeichens von d automatisch machen würdest. Bei Plus nach oben, bei Minus nach unten.
1. Bsp.:
Wie entsteht der Graph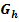 
der Funktion 
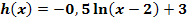aus dem Graph 
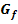der Funktion 
?
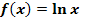Lösung:
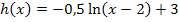
Es gilt somit: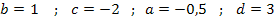 
Der Graph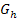 
der Funktion 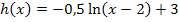entsteht aus dem Graph 
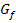der Funktion 
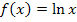durch folgende Abbildungen:
- Keine Spiegelung an der y-Achse (weil b positiv ist)
- Keine Stauchung/Streckung entlang der x-Achse, weil b = 1
- Verschiebung um 2 nach rechts (weil c negativ ist)
- Spiegelung an der x-Achse (weil a negativ ist)
- Stauchung mit dem Faktor 0,5 entlang der y-Achse
- Verschiebung um 3 nach oben (weil d positiv ist)
2. Bsp.:
Wir betrachten die Funktion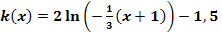 
. Durch welche Abbildungen entsteht der Graph 
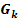der Funktion 
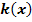aus dem Graph 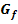der Funktion 
?
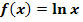Lösung:
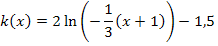
Es gilt somit: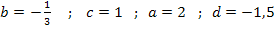 
Der Graph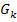 
der Funktion 
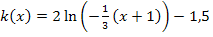entsteht aus dem Graph 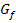der Funktion 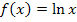durch folgende Abbildungen:
- Spiegelung an der y-Achse (weil b negativ ist)
- Streckung entlang der x-Achse mit dem Faktor
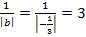
- Verschiebung um 1 nach links (weil c positiv ist)
- Keine Spiegelung an der x-Achse (weil a positiv ist)
- Streckung mit dem Faktor 2 entlang der y-Achse
- Verschiebung um 1,5 nach unten (weil d negativ ist)
Was tun, wenn die Funktion nicht in der benötigten Form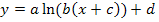 
gegeben ist?
Falls hinter dem ln nur eine einzelne Klammer steht, also wenn der Koeffizient b noch nicht ausgeklammert ist, solltest du auf jeden Fall b im Argument des ln ausklammern und die Funktion selbst dadurch auf genau die Form 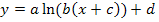bringen!
3. Bsp.:
Gegeben ist die Funktion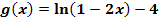 
. Durch welche Abbildungen entsteht der Graph 
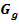der Funktion 
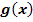aus dem Graph 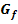der Funktion ?
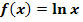Lösung:
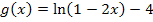
Die Funktion hat noch nicht die Form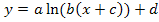 
. Um herauszufinden, wie sich der Graph 
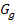der Funktion 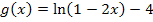aus dem Graph 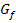der Funktion 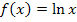ergibt, bringen wir die Funktion 
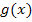vorab auf die Form 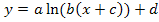. Dazu vertauschen wir zuerst beim Argument des ln die Reihenfolge und klammern dann den Faktor -2 im Argument des ln aus. Dadurch ergibt sich:
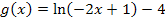
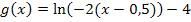
Es gilt somit: 
