Einführung des natürlichen Logarithmus, kurz ln
Der natürliche Logarithmus (logarithmus naturalis), abgekürzt ln ist der Logarithmus zur Basis e, wobei e für die Eulersche Zahl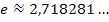 
steht. Wir schreiben also an Stelle von 
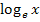einfach 
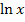. Damit ist hoffentlich klar:lnx ist gleichbedeutend mit 
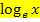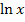. ist also bloßeine Kurzschreibweise für .
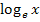Das ist so ähnlich wie bei lgx und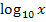 
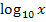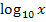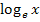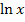. lgx ist bekanntlich eine Kurzschreibweise für den Zehnerlogarithmus . Für den Logarithmus zur Basis 10 schreibt man also oder kürzer lgx. Dagegen schreibt man für den Logarithmus zur Basis e eben oder . Wie schon gesagt, stellt 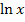eine Kurzschreibweise für den Logarithmus zur Basis e dar.
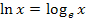
Die Schreibweise 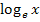wird jedoch extrem selten verwendet. Eigentlich wird stattdessen immer 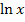geschrieben. Ab sofort werden wir daher nur noch die Schreibweise 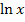für den natürlichen Logarithmus (logarithmus naturalis), also für den Logarithmus zur Basis e verwenden.
Den ln braucht man zum Beispiel, um Gleichungen der Form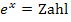 
nach dem Exponenten x aufzulösen. Außerdem gibt es auch Gleichungen der Form 
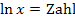. Wie man solche Gleichungen nach x auflöst, wird in diesem Kapitel erklärt. Außerdem wird die Funktion 
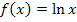eingeführt und gezeigt, wie man ihren Funktionsterm verändern muss, um ihren Graph an einer Achse zu spiegeln, ihn zu stauchen oder zu strecken und eventuell auch zu verschieben.
2a. Gleichungen mit lnx oder 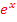 lösen, einschließlich ln-Rechengesetze
2c. Die ln-Funktion spiegeln, stauchen/strecken und verschieben |
