Das Wichtigste zur e-Funktion
Lösung:
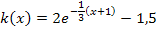
Es gilt somit: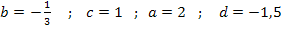 
Der Graph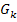 
der Funktion 
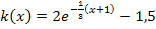entsteht aus dem Graph 
der Funktion 
durch folgende Abbildungen:
- Spiegelung an der y-Achse (weil b negativ ist)
- Streckung entlang der x-Achse mit dem Faktor
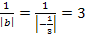
- Verschiebung um 1 nach links (weil c positiv ist)
- Keine Spiegelung an der x-Achse (weil a positiv ist)
- Streckung mit dem Faktor 2 entlang der y-Achse
- Verschiebung um 1,5 nach unten (weil d negativ ist)
Was aber tun, wenn die Funktion noch nicht ganz die benötigte Form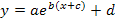 
hat?
Falls im Exponenten noch keine Klammer steht, also wenn der Koeffizient b noch nicht ausgeklammert ist, musst du die Funktion vorweg selbst auf die Form 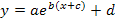bringen! Du musst dann vorher b im Exponenten ausklammern! (Wenn du das nämlich nicht machst, ist die Reihenfolge b, c , a , d der Abbildungen nämlich nicht mehr korrekt!)
3. Bsp.:
Durch welche Abbildungen entsteht der Graph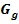 
der Funktion 
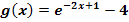aus dem Graph 
der Funktion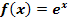 
?
Lösung:
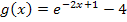
Die Funktion hat noch die Form 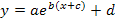. Um herauszufinden, wie sich der Graph 
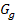der Funktion 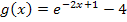aus dem Graph der Funktion ergibt, klammern wir vorweg den Faktor -2 im Exponenten aus. Dadurch ergibt sich:
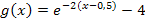
Es gilt somit: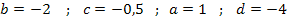 
Damit lässt sich leicht sagen, durch welche Abbildungen der Graph 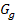aus dem Graph der Funktion entsteht:
- Spiegelung an der y-Achse (weil b negativ ist)
- Stauchung entlang der x-Achse mit dem Faktor
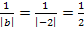
- Verschiebung um 0,5 nach rechts (weil c negativ ist)
- Keine Spiegelung an der x-Achse und keine Stauchung oder Streckung entlang der y-Achse (wegen a =1)
- Verschiebung um 4 nach unten (weil d negativ ist)
Nun versuche es doch gleich mal selbst an den Aufgaben des nächsten Beispiels!
4. Bsp.:
Durch welche Abbildungen entstehen die Graphen der folgenden Funktionen jeweils aus dem Graph 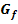der Funktion ?
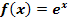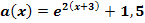
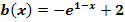
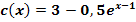
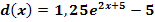
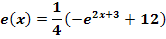
Lösung:
Beachte, dass die Funktionen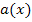 
bis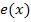 
noch nicht alle in der Form 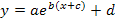gegeben sind! Bei manchen musst du selbst vorweg entweder an der Reihenfolge etwas ändern, insgesamt ausmultiplizieren oder eventuell im Exponenten b ausklammern, um sie auf die Form 
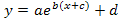zu bringen.
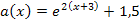
Die Funktion a steht bereits in der Form 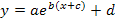da. Man kann also direkt ablesen:
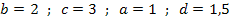
Der Graph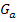 
der Funktion 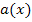entsteht deshalb durch folgende Abbildungen aus dem Graph der Funktion :
- Keine Spiegelung an der y-Achse (weil b positiv ist)
- Stauchung entlang der x-Achse mit dem Faktor
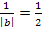
- Verschiebung um 3 nach links (weil c positiv ist)
- Keine Spiegelung an der x-Achse und keine Streckung/Stauchung entlang der y-Achse, wegen
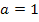
- Verschiebung um 1,5 nach oben (weil d positiv ist)
