Analysis = Infinitesimalrechnung » Die e-Funktion und ihre Umkehrfunktion die ln-Funktion » Das Wichtigste zur e-Funktion

Das Wichtigste zur e-Funktion

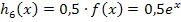
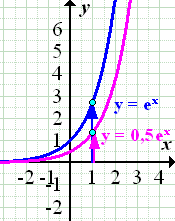
Stauchung bzw. Streckung von 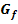entlang der x-Achse: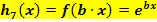

Dabei gilt: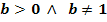

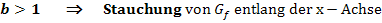
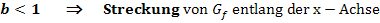
(Der Graph der Funktion 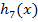entsteht, wenn man entlang der x-Achse mit dem Faktor 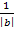staucht oder streckt.)

1. Bsp.:Stauchung von entlang der x-Achse durch b = 2, also mit dem Faktor :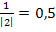

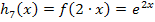
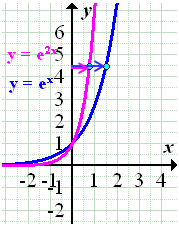
2. Bsp.:Streckung von entlang der x-Achse durch b = 0,5, also mit dem Faktor :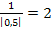

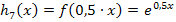
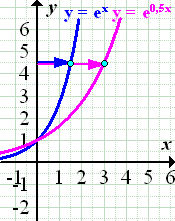
Nun alles auf einmal:Durch welche Abbildungen entsteht aus dem Graph der Funktion der Graph der Funktion ?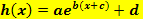

Wichtig:Die im Folgenden beschriebenen Abbildungen müssen in genau der angegebenen Reihenfolge durchgeführt werden, ansonsten wird das Ergebnis eventuell falsch! Wir arbeiten uns systematisch von innen nach außen vor:Von b, über c und a bis zum d.

Merke:Abbildungen immer in der Reihenfolge b,  c , a , d

  • Spiegelung an der y-Achse (nur wenn b negativ ist)
  • Stauchung/Streckung entlang der x-Achse mit dem Faktor
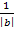
  • Verschiebung um 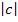zur Seite (nach links, wenn c positiv ist – nach rechts, wenn c negativ ist)
  • Spiegelung an der x-Achse (nur wenn a negativ ist)
  • Stauchung/Streckung entlang der x-Achse mit dem Faktor
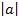
  • Verschiebung um 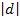in y-Richtung (nach oben, wenn d positiv ist – nach unten, wenn d negativ ist)

Zum Koeffizienten b

Ist der Koeffizient b negativ, muss der Graph als erstes an der y-Achse gespiegelt werden. Anschließend wird mit dem Faktor 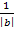entlang der x-Achse gestreckt bzw. gestaucht (außer für b = -1).

Für b = -1, d.h. wenn der Funktionsterm die Form 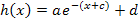hat,  muss der Graph nur an der y-Achse gespiegelt werden;eine Stauchung oder Streckung entlang der x-Achse entfällt in diesem Fall.

Für 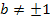:D er Faktor, mit dem man entlang der x-Achse stauchen bzw. strecken muss, ist der positive Kehrwert von b.

Daraus ergibt sich:

Für 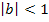:  Streckung des Graphen entlang der x-Achse

Für 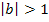:  Stauchung des Graphen entlang der x-Achse

Ist beispielsweise b = 2, muss der Graph mit dem Faktor 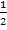entlang der x-Achse gestaucht werden. Anderes Beispiel:Für 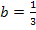muss der Graph mit dem Faktor 3 entlang der x-Achse gestreckt werden.

Ist der Faktor b positiv entfällt die Spiegelung an der y-Achse und man führt gleich die Streckung bzw. Stauchung entlang der x-Achse durch, außer für b = 1.

Für b = 1, d.h. wenn der Funktionsterm die Form 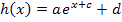hat, muss weder an der y-Achse gespiegelt noch entlang der x-Achse gestaucht oder gestreckt werden.

Zum Koeffizienten c

0
0
0
0