Das Wichtigste zur e-Funktion
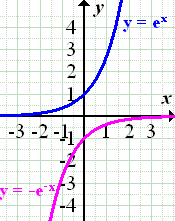
Das waren jetzt die wichtigsten Dinge zur natürlichen Exponentialfunktion. Auf die Untersuchung des Symmetrieverhaltens wurde absichtlich verzichtet, da die e-Funktion sowieso keine Symmetrie aufweist. Das gleiche gilt für die Berechnung der Nullstellen. Der Graph verläuft immer oberhalb der x-Achse und schneidet oder berührt die x-Achse nie. Deshalb hat die e-Funktion 
keine Nullstellen.
Wir fassen noch einmal das Wichtigste zur e-Funktion übersichtlich zusammen:
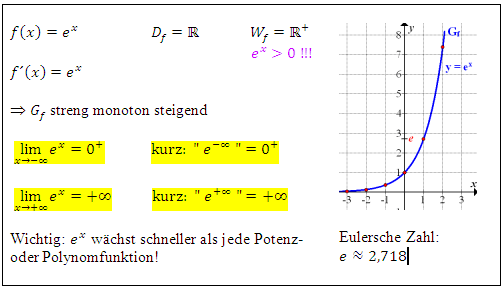
Der Graph 
der Funktion kann durch verschiedene Abbildungen verändert werden, z.B. durch Spiegelung an einer Achse oder Spiegelung am Ursprung, Verschiebung nach oben oder unten bzw. zur Seite nach links oder rechts und eventuell Stauchung oder Streckung entlang einer Koordinatenachse. Wie muss der Funktionsterm verändert werden, damit durch eine oder mehrere dieser Abbildungen entsteht?
Als erstes wollen wir immer nur eine einzige Abbildung durchführen. Nachher schauen wir uns an, was man mit dem Funktionsterm machen muss, um gleich mehrere Abbildungen nacheinander durchzuführen. Wir gehen dabei jeweils vom Graph der Funktion aus.
Spiegelung von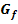 
an der x-Achse: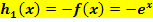 
(Der rosafarbene Graph der Funktion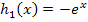 
entsteht, wenn man den blauen Graph der Funktion an der x-Achse spiegelt.)
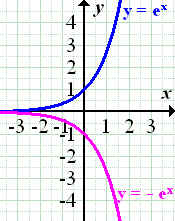
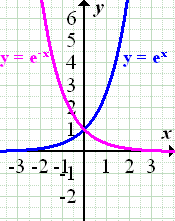
Spiegelung von 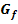an der y-Achse: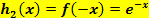 
(Der rosafarbene Graph der Funktion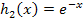 
entsteht, wenn man den blauen Graph der Funktion an der y-Achse spiegelt.)
Spiegelung von 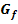am Ursprung: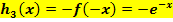 
(Der rosafarbene Graph der Funktion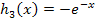 
entsteht, wenn man den blauen Graph der Funktion am Ursprung spiegelt. Das entspricht auch einer Spiegelung an x- und y-Achse.)
Verschiebung von 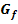nach oben oder unten: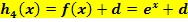 
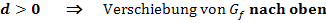
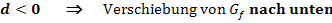
(Der Graph der Funktion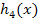 
entsteht, wenn man um d nach oben oder unten verschiebt.)
1. Bsp.:Verschiebung von um 2 nach oben:
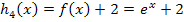
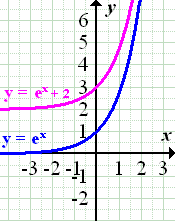
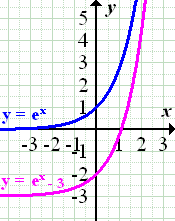
2. Bsp.:Verschiebung von um 3 nach unten:
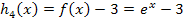
Verschiebung von 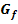nach links oder rechts: 
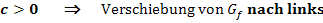
(Der Graph der Funktion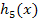 
entsteht, wenn man um c nach links oder rechts verschiebt.)
1. Bsp.:Verschiebung von um 1 nach links:
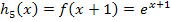
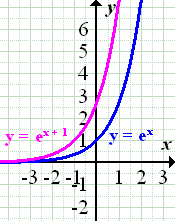
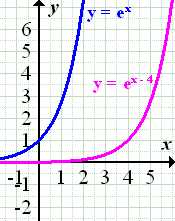
2. Bsp.:Verschiebung von um 4 nach rechts:
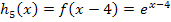
Stauchung bzw. Streckung von 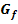entlang der y-Achse: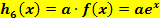 
Dabei gilt: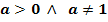 
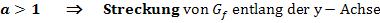
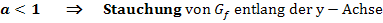
(Der Graph der Funktion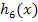 
entsteht, wenn man entlang der y-Achse mit dem Faktor a staucht oder streckt.)
1. Bsp.:Streckung von entlang der y-Achse mit dem Faktor 2:
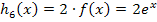
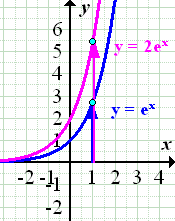
2. Bsp.:Stauchung von entlang der y-Achse mit dem Faktor 0,5:
