Das Wichtigste zur e-Funktion
Daher gilt:
Anschaulich bedeutet dies, dass der Graph 
für x gegen 
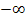die x-Achse (y = 0) als waagrechte Asymptote hat. Der Graph schmiegt sich an die x-Achse an, schneidet sie jedoch nie.
Die Annäherung von an die x-Achse erfolgt dabei von oben, was durch die Schreibweise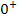 
ausgedrückt wird. Dass der Graph immer oberhalb der x-Achse verläuft, sieht man an der Abbildung oben!
Wertemenge der Funktion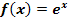 
:
Die Wertemenge umfasst alle Zahlen, die für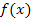 
bzw. y herauskommen können. Weil der Graph der natürlichen Exponentialfunktion immer oberhalb der x-Achse liegt, können bei 
ausschließlich positive Zahlen 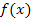bzw. y herauskommen. Die Wertemenge lautet daher:
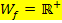
Wir halten noch einmal fest: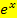 
ist immer positiv, unabhängig davon, was für x eingesetzt wird!
Merke:„e hoch egal was“ ist immer positiv! So sind beispielsweise auch die Ausdrücke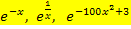 
grundsätzlich positiv. Auch wenn der Exponent negativ ist, ist „e hoch irgendwas“ immer positiv. Das ist super, super wichtig!!!
Ableitung der Funktion 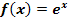und ihr Monotonieverhalten:
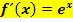
Funktionsterm und Ableitung der natürlichen Exponentialfunktion sind also identisch! Das ist etwas Besonderes. Die e-Funktion ist tatsächlich die einzige Funktion, welche die Gleichung 
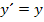bzw.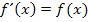 
erfüllt. (Den mathematischen Beweis dieser Aussage ersparen wir uns lieber;der Beweis ist nicht so leicht und du brauchst ihn sowieso nicht.)
Anschaulich bedeutet die Gleichung 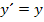bzw. 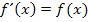, dass die Steigung 
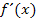an einer bestimmten Stelle x genau dem Funktionswert 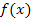, also der y-Koordinate des jeweiligen Kurvenpunkts entspricht. Steigung und Funktionswert an einer bestimmten Stelle verhalten sich nicht nur direkt proportional, sondern sind sogar ganz gleich! Da mit zunehmendem x die Funktionswerte 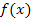stark zunehmen, nimmt also auch die Steigung immer mehr zu. Der Graph verläuft umso steiler, desto größer x wird.
Wegen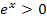 
für x 
ℝ gilt: 
Wegen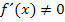 
existieren keine Extrema oder Terrassenpunkte.
Nur für Schüler, die im Unterricht bereits die zweite Ableitung besprochen haben:
Entsprechend gilt für die zweite Ableitung: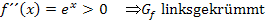 
Wegen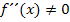 
existieren keine Wendepunkte.
Stammfunktion zu :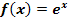
Bei einer Stammfunktion F(x) muss bekanntlich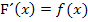 
gelten. Die Menge aller Stammfunktionen zu lautet daher:
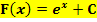
Wenn man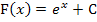 
ableitet, fällt die additive Konstante C weg und es ergibt sich wieder . Die Bedingung 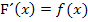ist offensichtlich erfüllt. Die Konstante C kann ohne weitere Informationen nicht exakt bestimmt werden.
