Das Wichtigste zur e-Funktion
Entsprechend ergibt sich für x = 4 der noch höhere Funktionswert: 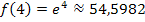
Daran siehst du, wie schnell die Funktionswerte von  mit wachsendem x zunehmen. Der Graph verläuft für große, positive x-Werte sehr steil. Betrachte dazu die folgende Abbildung!
mit wachsendem x zunehmen. Der Graph verläuft für große, positive x-Werte sehr steil. Betrachte dazu die folgende Abbildung!
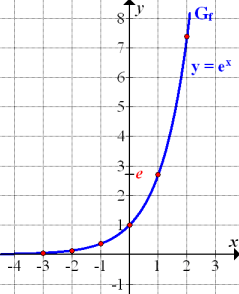
Abb.:Graph  der natürlichen Exponentialfunktion
der natürlichen Exponentialfunktion 
Schnittpunkt mit der y-Achse:
Die e-Funktion schneidet die y-Achse offensichtlich im Punkt (0|1). Das folgt aus:
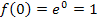
Schnittpunkte mit der x-Achse, Nullstellen:
Es existieren keine Schnittpunkte der e-Funktion mit der x-Achse, also keine Nullstellen. Der Graph  schmiegt sich für x gegen
schmiegt sich für x gegen 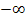 zwar beliebig nah an die x-Achse an, schneidet sie jedoch nie. (Die x-Achse ist für x gegen
zwar beliebig nah an die x-Achse an, schneidet sie jedoch nie. (Die x-Achse ist für x gegen 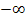 waagrechte Asymptote. Obwohl es in der Abbildung oben so wirkt, als würde der Graph der e-Funktion die x-Achse berühren, ist das in Wirklichkeit nicht der Fall.
waagrechte Asymptote. Obwohl es in der Abbildung oben so wirkt, als würde der Graph der e-Funktion die x-Achse berühren, ist das in Wirklichkeit nicht der Fall.  liegt immer oberhalb der x-Achse und kommt niemals ganz an die x-Achse heran!)
liegt immer oberhalb der x-Achse und kommt niemals ganz an die x-Achse heran!)
Verhalten von 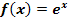 an den Rändern der Definitionsmenge:
an den Rändern der Definitionsmenge:
An Hand des Graphen überlegen wir uns nun das Verhalten von  an den Rändern der Definitionsmenge
an den Rändern der Definitionsmenge 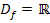 , also das Verhalten von
, also das Verhalten von  für x gegen
für x gegen 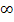 und
und 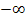 . (Definitionslücken gibt es hier schließlich keine. Daher entspricht hier das Verhalten an den Rändern von
. (Definitionslücken gibt es hier schließlich keine. Daher entspricht hier das Verhalten an den Rändern von 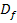 dem Verhalten im Unendlichen.)
dem Verhalten im Unendlichen.)
Man erkennt, dass  für sehr große x extrem große Funktionswerte y annimmt. Daher gilt:
für sehr große x extrem große Funktionswerte y annimmt. Daher gilt:

Wichtig:Die e-Funktion wächst schneller als jede Potenzfunktion und schneller als jedes Polynom, d.h. sie geht für große x schneller gegen Unendlich als beispielsweise die Potenzfunktionen 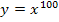 oder
oder 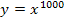 ! Für x gegen Unendlich gehen auch
! Für x gegen Unendlich gehen auch 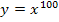 oder
oder 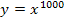 gegen Unendlich, aber eben nicht so schnell wie die Funktion
gegen Unendlich, aber eben nicht so schnell wie die Funktion  . Auf der Tatsache, dass die natürliche Exponentialfunktion schneller wächst als jede Potenz- oder Polynomfunktion, basieren die Berechnungen vieler schwieriger Grenzwerte mit
. Auf der Tatsache, dass die natürliche Exponentialfunktion schneller wächst als jede Potenz- oder Polynomfunktion, basieren die Berechnungen vieler schwieriger Grenzwerte mit 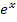 . (Siehe Abschnitt:Grenzwerte von e- und ln-Funktionen)
. (Siehe Abschnitt:Grenzwerte von e- und ln-Funktionen)
Nun zum Verhalten von  für x gegen
für x gegen 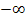 :Bereits an der oben gezeigten Wertetabelle erkennt man, dass sich die y-Werte immer mehr an die Zahl Null annähern, wenn man für x immer kleinere (stark negative) Zahlen einsetzt. Für sehr kleine x ergeben sich also y-Werte, die nahezu Null sind. (Mit „sehr klein“ ist hier gemeint, dass die x-Werte ganz weit links auf der Zahlengeraden liegen, also x gegen
:Bereits an der oben gezeigten Wertetabelle erkennt man, dass sich die y-Werte immer mehr an die Zahl Null annähern, wenn man für x immer kleinere (stark negative) Zahlen einsetzt. Für sehr kleine x ergeben sich also y-Werte, die nahezu Null sind. (Mit „sehr klein“ ist hier gemeint, dass die x-Werte ganz weit links auf der Zahlengeraden liegen, also x gegen 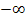 .) Auch an den berechneten Werten für x = -3 und x = -2 ist das schon zu erkennen.
.) Auch an den berechneten Werten für x = -3 und x = -2 ist das schon zu erkennen. 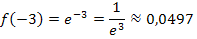
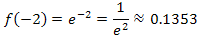
Die Funktionswerte für x gegen 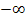 gehen also gegen Null;sie bleiben aber immer positiv.
gehen also gegen Null;sie bleiben aber immer positiv.

