Das Wichtigste zur e-Funktion

(Die Eulersche Zahl e ist nach dem berühmten Mathematiker Leonhard Euler benannt.)

Mit der Zahl e ist es so ähnlich wie bei der Kreiszahl 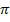, die du bestimmt kennst. Auch 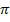ist eine Naturkonstante. Du weißt bestimmt, dass 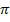immer bei Berechnungen am Kreis oder bei rotationssymmetrischen Körpern (Kugel, Kegel, Zylinder etc.) vorkommt. Entsprechend kommt die Zahl e oft im Zusammenhang mit Wachstums- oder Zerfallsprozessen vor. Aber auch in anderem mathematischen Zusammenhang stößt man immer wieder auf die Zahl e, so zum Beispiel bei dem oben schon erwähnten Grenzwert 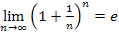oder bei der unendlichen Reihe .

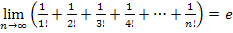Nun aber wieder zurück zur e-Funktion .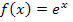

Definitionsmenge der Funktion :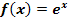

Wie lautet die maximale Definitionsmenge von ? Welche Zahlen darf man für x einsetzen? Oder anders herum gefragt:Gibt es irgendwelche Zahlen, die man nicht für x einsetzen darf? Überlege erst mal selbst! (Stelle dir bei deiner Überlegung die Zahl e zur Vereinfachung als 2,7 vor: )

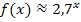Dass man beliebige positive Zahlen einsetzen darf, ist dir vermutlich von selbst klar. Doch wie sieht es mit negativen Zahlen und mit der Null aus? Beginnen wir mit der Zahl Null. Was ergibt 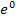bzw. 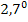? Ist das überhaupt definiert?

Klar ist das definiert! Jede beliebige positive Zahl hoch Null ergibt 1! Daher gilt auch: 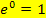bzw.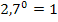

Die Zahl Null können wir also problemlos bei für x einsetzen. Nun weiter mit den negativen Zahlen. Kann man „e hoch eine Minus-Zahl“ rechnen bzw. „2,7 hoch eine Minus-Zahl“?

Tipp:Denk dabei an das Potenzgesetz:

Aus diesem Potenzgesetz folgt, dass man sehr wohl bei auch negative Zahlen für x einsetzen kann. Was ergibt sich beispielsweise für x = -3, x = -2 oder für x = -1?

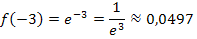
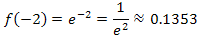
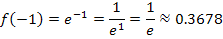
Man kann also bei beliebige reelle Zahlen, d.h. alle positiven und negativen Zahlen einschließlich der Null, für x einsetzen. Die maximale Definitionsmenge der Funktion lautet demnach:

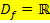
Graph der natürlichen Exponentialfunktion

Wie sieht denn nun der Graph der Funktion aus? Um ihn zeichnen zu können, erstellen wir eine Wertetabelle im Bereich [-3;2] mit 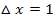. (Mit 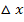ist die Schrittweite gemeint, d.h. man soll hier die Zahlen -3;-2;-1, 0, 1 und 2 in 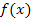einsetzen.)

x	-3	-2	-1	0	1	2

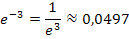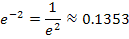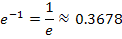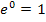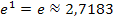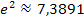Warum haben wir bereits bei x = 2 aufgehört und keine höheren Werte, wie zum Beispiel x = 3 oder x = 4 in eingesetzt? Ganz einfach:Die e-Funktion steigt für große x-Werte extrem steil an. Bei x = 3 ergibt sich bereits 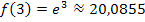und der zugehörige Kurvenpunkt passt gar nicht mehr in unser Koordinatensystem.

---