Das Wichtigste zur e-Funktion
Der zu 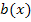 gehörige Graph muss demnach bei y = 1 eine waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt genau einer der dargestellten Graphen, nämlich der dunkelblaue Graph. Der dunkelblaue Graph gehört zu
gehörige Graph muss demnach bei y = 1 eine waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt genau einer der dargestellten Graphen, nämlich der dunkelblaue Graph. Der dunkelblaue Graph gehört zu 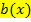 .
.
Der Graph der Funktion 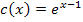 ergibt sich aus dem Graph der Funktion
ergibt sich aus dem Graph der Funktion 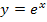 durch Verschiebung um 1 nach rechts. Der zu
durch Verschiebung um 1 nach rechts. Der zu 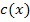 gehörige Graph muss demnach die x-Achse als waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt genau der hellblaue Graph. Der hellblaue Graph gehört zu
gehörige Graph muss demnach die x-Achse als waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt genau der hellblaue Graph. Der hellblaue Graph gehört zu 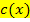 .
.
Der Graph der Funktion 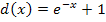 ergibt sich aus dem Graph der Funktion
ergibt sich aus dem Graph der Funktion 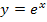 durch Spiegelung an der y-Achse und Verschiebung um 1 nach oben. Der zu
durch Spiegelung an der y-Achse und Verschiebung um 1 nach oben. Der zu 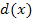 gehörige Graph muss demnach bei y = 1 eine waagrechte Asymptote besitzen und streng monoton fallend sein. Dies erfüllt genau einer der dargestellten Graphen, nämlich der rote Graph. Der rote Graph gehört zu
gehörige Graph muss demnach bei y = 1 eine waagrechte Asymptote besitzen und streng monoton fallend sein. Dies erfüllt genau einer der dargestellten Graphen, nämlich der rote Graph. Der rote Graph gehört zu 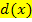 .
.
Der Graph der Funktion 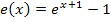 ergibt sich aus dem Graph der Funktion
ergibt sich aus dem Graph der Funktion 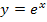 durch Verschiebung um 1 nach links und um 1 nach unten. Der zu
durch Verschiebung um 1 nach links und um 1 nach unten. Der zu 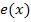 gehörige Graph muss demnach bei y = -1 eine waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt nur der grüne Graph. Der grüne Graph gehört zu
gehörige Graph muss demnach bei y = -1 eine waagrechte Asymptote besitzen und streng monoton steigend sein. Dies erfüllt nur der grüne Graph. Der grüne Graph gehört zu 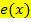 .
.
Hoffentlich hast du nun verstanden, wie sie der Graph 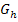 einer Funktion der Form
einer Funktion der Form 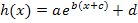 aus dem Graph
aus dem Graph  der Funktion
der Funktion 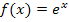 ergibt. Die Funktion h kann allgemein als
ergibt. Die Funktion h kann allgemein als 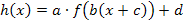 aufgefasst werden. Man entwickelt den Graph
aufgefasst werden. Man entwickelt den Graph 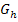 schrittweise aus dem Graph
schrittweise aus dem Graph  .
.
Zum Abschluss dieses Teils noch eine Übersicht der Abbildungen, die in der gezeigten Reihenfolge aus dem Graph  der Funktion
der Funktion  den Graphen
den Graphen 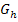 der Funktion
der Funktion 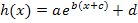 machen:
machen:
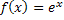
|
Falls b <0:
Spiegelung von und Streckung/Stauchung entlang der x-Achse mit dem Faktor für für |
Falls b >0:
Keine Spiegelung von nur Streckung/Stauchung entlang der x-Achse mit dem Faktor für für |
|||
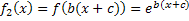
|
Falls c <0:
Verschiebung von |
Falls c >0:
Verschiebung von |
|||
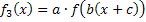
|
Falls a <0:
Spiegelung von und Streckung/Stauchung entlang der y-Achse mit dem Faktor für für |
Falls a >0:
Keine Spiegelung von nur Streckung/Stauchung von für für |
|||
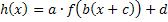
|
Falls d <0:
Verschiebung von |
Falls d >0:
Verschiebung von |
Nach dem gleichen Prinzip kann nicht nur der Graph der Funktion  gespiegelt, gestaucht bzw. gestreckt und verschoben werden. Das kann man auch mit anderen Funktionen
gespiegelt, gestaucht bzw. gestreckt und verschoben werden. Das kann man auch mit anderen Funktionen 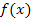 machen. Du kennst das sicherlich schon von der Sinusfunktion
machen. Du kennst das sicherlich schon von der Sinusfunktion 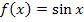 . In der 10. Klasse habt ihr in der Schule bestimmt darüber gesprochen, wie sich der Graph
. In der 10. Klasse habt ihr in der Schule bestimmt darüber gesprochen, wie sich der Graph 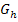 der Funktion
der Funktion 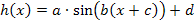 aus dem Graph der Sinusfunktion
aus dem Graph der Sinusfunktion 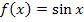 entwickeln lässt. (Mehr zur allgemeinen Sinusfunktion
entwickeln lässt. (Mehr zur allgemeinen Sinusfunktion 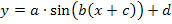 im Kapitel:Trigonometrische Funktionen:Sinus -, Kosinus – und Tangensfunktion) Es steckt hierin also ein generelles Prinzip. Mehr dazu auch im Kapitel:Funktionen spiegeln, verschieben, stauchen oder strecken
im Kapitel:Trigonometrische Funktionen:Sinus -, Kosinus – und Tangensfunktion) Es steckt hierin also ein generelles Prinzip. Mehr dazu auch im Kapitel:Funktionen spiegeln, verschieben, stauchen oder strecken
- Page 12 of 12
- « Previous
- 9
- 10
- 11
- 12
- Next »

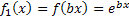
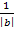
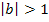 :Stauchung
:Stauchung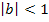 :Streckung
:Streckung
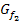 um
um 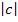
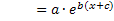
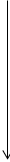
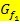
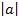
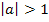 :Streckung
:Streckung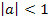 :Stauchung
:Stauchung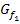 an der x-Achse
an der x-Achse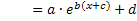
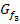 um
um