Das Wichtigste zur e-Funktion
Welche Abbildung muss durchgeführt werden, um vom Graph 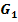 der Funktion
der Funktion 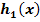 zum Graph
zum Graph 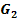 der Funktion
der Funktion 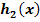 zu kommen, welche um vom Graph
zu kommen, welche um vom Graph 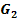 der Funktion
der Funktion 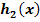 zum Graph
zum Graph 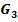 der Funktion
der Funktion 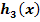 zu kommen usw. bis zum Graph
zu kommen usw. bis zum Graph 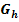 der Funktion
der Funktion 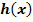 ?
?
Lösung:
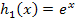
Verschiebung von rechts ergibt |
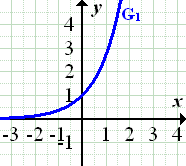 |
|||
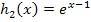
Stauchung von y-Achse mit dem Faktor 0,5 ergibt |
 |
|||

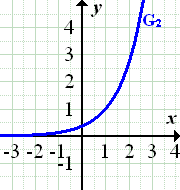
Verschiebung von unten ergibt |
 |
|||
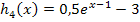
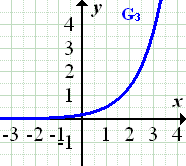
Spiegelung des unterhalb der x-Achse liegenden Teils von an der x-Achse ergibt |
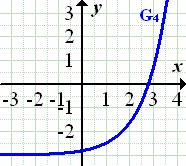 |
|||
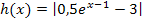 |
 |
Sehr häufig finden sich in Prüfungen auch Aufgaben, bei denen du einigen gegebenen Graphen den jeweils zugehörigen Funktionsterm zuordnen musst.
6. Bsp.:Graphen zuordnen
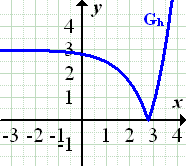
Gegeben sind die Funktionen:
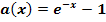
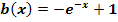
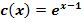
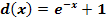
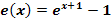
In der nachfolgenden Abbildung sind die Graphen dieser Funktionen dargestellt. Welcher Graph gehört zu welcher Funktion?
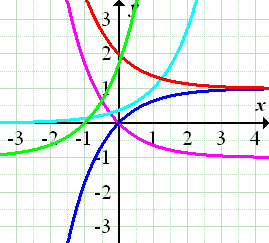
Lösung:


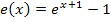
Um herauszufinden, welcher Graph zu welcher Funktion gehört, solltest du bei jeder der angegebenen Funktionen überlegen, durch welche Abbildung(en) ihr Graph aus dem Graph der Funktion 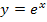 hervorgeht. Dadurch kannst du auf die waagrechte Asymptote und das Steigungsverhalten der gegebenen Funktion schließen. Stelle dir dazu als erstes den Graph von
hervorgeht. Dadurch kannst du auf die waagrechte Asymptote und das Steigungsverhalten der gegebenen Funktion schließen. Stelle dir dazu als erstes den Graph von 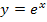 vor und überlege dir, wie dann der entsprechend gespiegelte bzw. verschobene Graph aussehen muss. So kannst du dann jeder der angegebenen Funktionen jeweils einen der abgebildeten Graphen eindeutig zuordnen.
vor und überlege dir, wie dann der entsprechend gespiegelte bzw. verschobene Graph aussehen muss. So kannst du dann jeder der angegebenen Funktionen jeweils einen der abgebildeten Graphen eindeutig zuordnen.
Rosa 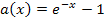
Dunkelblau 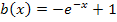
Hellblau 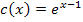
Rot 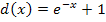
Grün 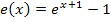
Erklärungen:
Der Graph der Funktion 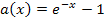 ergibt sich aus dem Graph der Funktion
ergibt sich aus dem Graph der Funktion 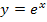 durch Spiegelung an der y-Achse und Verschiebung um 1 nach unten. Die Funktion
durch Spiegelung an der y-Achse und Verschiebung um 1 nach unten. Die Funktion 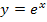 hat bekanntlich für
hat bekanntlich für 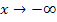 die x-Achse y = 0 als waagrechte Asymptote und ist streng monoton steigend. Wegen der Spiegelung an der y-Achse muss
die x-Achse y = 0 als waagrechte Asymptote und ist streng monoton steigend. Wegen der Spiegelung an der y-Achse muss 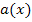 streng monoton fallend sein. Wegen der Verschiebung um 1 nach unten muss die waagrechte Asymptote von
streng monoton fallend sein. Wegen der Verschiebung um 1 nach unten muss die waagrechte Asymptote von 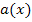 bei y = -1 liegen. Die waagrechte Asymptote von a gilt allerdings nur für
bei y = -1 liegen. Die waagrechte Asymptote von a gilt allerdings nur für 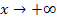 , weil der Graph von a schließlich durch Spiegelung an der y-Achse aus dem Graph von
, weil der Graph von a schließlich durch Spiegelung an der y-Achse aus dem Graph von 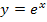 hervorgeht. Der zu
hervorgeht. Der zu 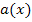 gehörende Graph muss demnach bei y = -1 eine waagrechte Asymptote besitzen und streng monoton fallend sein. Diese Bedingungen erfüllt nur einer der dargestellten Graphen, nämlich der rosafarbene. Der rosa Graph gehört zu
gehörende Graph muss demnach bei y = -1 eine waagrechte Asymptote besitzen und streng monoton fallend sein. Diese Bedingungen erfüllt nur einer der dargestellten Graphen, nämlich der rosafarbene. Der rosa Graph gehört zu 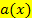 .
.
Der Graph der Funktion 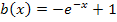 ergibt sich aus dem Graph der Funktion
ergibt sich aus dem Graph der Funktion 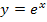 durch Spiegelung an der x- und y-Achse sowie durch Verschiebung um 1 nach oben.
durch Spiegelung an der x- und y-Achse sowie durch Verschiebung um 1 nach oben.

 um 1 nach
um 1 nach
 .
.
 .
.
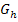 .
.