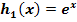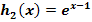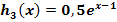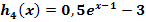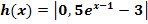Das Wichtigste zur e-Funktion
Du erhältst den Graph  auch, wenn du den Graph
auch, wenn du den Graph  der Funktion
der Funktion  folgendermaßen abbildest:
folgendermaßen abbildest:
· Spiegelung von  an der x-Achse;das ergibt den Graph
an der x-Achse;das ergibt den Graph  der Funktion
der Funktion 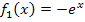
· Verschiebung von 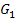 um 3 nach links;das ergibt den Graph
um 3 nach links;das ergibt den Graph 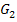 der Funktion
der Funktion 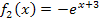
· Stauchung von 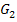 entlang der x-Achse mit dem Faktor
entlang der x-Achse mit dem Faktor 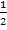 ;das ergibt den Graph
;das ergibt den Graph 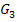 der Funktion
der Funktion 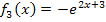
· Verschiebung von 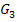 um 12 nach oben;das ergibt den Graph
um 12 nach oben;das ergibt den Graph  der Funktion
der Funktion 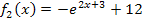
· Stauchung von  entlang der y-Achse mit dem Faktor
entlang der y-Achse mit dem Faktor 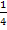 ;das ergibt den Graph
;das ergibt den Graph 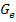 der Funktion
der Funktion 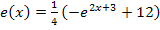
Woher weißt du, in welcher Reihenfolge die jeweiligen Abbildungen durchgeführt werden müssen? Dazu musst du dich fragen, welche Funktionen jeweils miteinander verkettet wurden und in welcher Reihenfolge dabei jeweils vorgegangen werden musste, um auf die angegebene Funktionsgleichung zu kommen. Dabei muss, wie gesagt, von „innen nach außen“ vorgegangen werden. Die innerste Funktion muss durch die erste Abbildung entstehen;die äußerste durch die letzte Abbildung. Die richtige Reihenfolge der Abbildungen zu erkennen, ist erfahrungsgemäßfür viele Schüler nicht leicht.
Wesentlich einfacher ist es für dich bestimmt, wenn du dich mit den Abbildungen in der oben besprochenen festen Reihenfolge b , c , a , d im Funktionsterm vorarbeiten kannst. Dafür musst du die Funktion aber immer vorher auf die Form 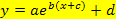 bringen. Nur wenn die Funktion in dieser Form dasteht, kannst du die Abbildungen in der Reihenfolge b , c , a , d durchführen. Das ist doch viel einfacher, als wenn du dir jedes Mal überlegen müsstest, welche Abbildung nach der Regel „von innen nach außen“ als erstes kommt und welche als nächstes. Daher den Funktionsterm besser zuerst auf die Form
bringen. Nur wenn die Funktion in dieser Form dasteht, kannst du die Abbildungen in der Reihenfolge b , c , a , d durchführen. Das ist doch viel einfacher, als wenn du dir jedes Mal überlegen müsstest, welche Abbildung nach der Regel „von innen nach außen“ als erstes kommt und welche als nächstes. Daher den Funktionsterm besser zuerst auf die Form 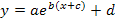 bringen und sich erst anschließend Gedanken über die nötigen Abbildungen machen, die aus dem Graph
bringen und sich erst anschließend Gedanken über die nötigen Abbildungen machen, die aus dem Graph  der Funktion
der Funktion  den Graph der Funktion
den Graph der Funktion 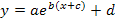 machen.
machen.
Abschließend noch ein kleiner Tipp zu e-Funktionen mit Betrag um den gesamten Funktionsterm herum:
Den Graph einer Funktion der Form 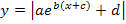 erhältst du, indem du nur den unterhalb der x-Achse liegenden Teil des Graphen der Funktion
erhältst du, indem du nur den unterhalb der x-Achse liegenden Teil des Graphen der Funktion 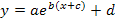 an der x-Achse nach oben spiegelst. Am oberhalb der x-Achse liegenden Teil des Graphen von
an der x-Achse nach oben spiegelst. Am oberhalb der x-Achse liegenden Teil des Graphen von 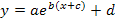 änderst du gar nichts. Es entsteht dadurch am Graph der für Betragsfunktionen typische „Knick“ an der Nullstelle.
änderst du gar nichts. Es entsteht dadurch am Graph der für Betragsfunktionen typische „Knick“ an der Nullstelle.
5. Bsp.:
Es soll der Graph 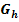 der Funktion
der Funktion 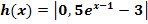 schrittweise aus dem Graph
schrittweise aus dem Graph 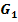 der Funktion
der Funktion 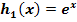 hergeleitet werden. Zeichne dazu die Graphen der folgenden Funktionen:
hergeleitet werden. Zeichne dazu die Graphen der folgenden Funktionen: