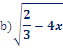Irrationale Zahlen, die Menge der reellen Zahlen und reinquadratische Gleichungen in der Menge ℝ

Lösung: In Mengenschreibweise:

D=

Oder in Intervallschreibweise:

D=

Da der Radikand, also der Ausdruck unter der Wurzel, immer positiv oder gleich Null sein muss, gilt:

Lösung:

D= Oder

D=

Erklärung:

 

D=

Oder

D=

Achtung: Vergiss nicht, dass die Division durch Null nicht definiert ist! Deshalb darf der Nenner niemals gleich Null sein! Da ergeben würde, darf der Radikand in diesem Fall nicht gleich Null sein, weil dann auch der Nenner Null werden würde. Weil die Wurzel im Nenner steht, gilt (anstatt von Radikand größer oder gleich Null) Radikand größer Null!

Lösung: D=G=ℝ

Erklärung:

Da wegen der geraden Potenz immer positiv oder gleich Null ist und dazu eine weitere Zahl (nämlich 1) addiert wird, kann der Radikand niemals negativ werden, egal was man für x einsetzt. Deshalb kann jede beliebige Zahl aus der Grundmenge G=ℝ für x eingesetzt werden. Für Schüler, die lieber rechnen wollen; empfiehlt sich folgender Lösungsweg:

Wegen der geraden Potenz ist immer positiv und daher auch immer größer (oder gleich) -1. Deshalb ist die Aussage immer wahr, egal was man für x einsetzt. Es gilt: D=G

Also in Worten: Die Definitionsmenge ist gleich der Grundmenge. Oft ist die Grundmenge allerdings nicht explizit angegeben, dann kann man davon ausgehen, dass G=ℝ gilt.

Lösung: D=

Oder in der Intervallschreibweise:

D=

Oder etwas anders ausgedrückt:

D=ℝ∖

Vorsicht: ist zwar wegen der geraden Potenz niemals negativ, aber hier wird von noch eine Zahl (nämlich 9) abgezogen. Deshalb kann man nicht –wie im vorherigen Beispiel- einfach davon ausgehen, dass der Radikand sowieso nicht negativ wird. Wir müssen daher die Ungleichung lösen.

Leider handelt es sich dabei um eine quadratische Ungleichung, d.h. eine Ungleichung mit . Diese Ungleichungen sind nicht ganz einfach zu lösen und machen vielen Schülern Probleme. Es gibt verschiedene Methoden, solche Ungleichungen zu lösen.

Das Thema quadratische Ungleichungen wird in einem anderen Kapitel dieses Programms noch ausführlicher behandelt werden. Deshalb soll im Folgenden nur eine relativ einfache Methode zur Lösung solcher Aufgaben gezeigt werden. Solltest du im Unterricht solche Aufgaben gar nicht behandelt haben, kannst du die Beispiele e), f) und g) auch überspringen, vor allem wenn du eine Realschule besuchst.

Nun müsste eigentlich die Wurzel gezogen werden, um nach x aufzulösen. Doch was passiert dann mit dem Ungleichheitszeichen?

Da sich diese Frage nicht so leicht beantworten lässt, wollen wir zur Vereinfachung zuerst die quadratische Gleichung lösen.

Achtung: nicht vergessen!

und

Nun stellst du dir am besten einen Zahlenstahl vor:

Jetzt ist noch die Frage zu beantworten, ob die Zahlen aus dem grünen Bereich, also , oder die Zahlen aus dem lila Bereich, also , die Ungleichung erfüllen. Am besten setzt du einige Zahlen aus den beiden Bereichen zur Probe ein und überprüfst, ob sich eine wahre Aussage ergibt. Wählt man z.B. die Zahl -4 (liegt im linken grünen Bereich) für x, so stellt man fest, dass die Ungleichung erfüllt ist, da und ergibt eine wahre Aussage. Das gleiche würde sich ergeben, wenn man +4(eine Zahl aus dem rechten grünen Bereich) für x einsetzt. Wählt man dagegen eine Zahl aus dem lilafarbenen Bereich, z.B. die Zahl 1 für x, ergibt sich ein Widerspruch: und nicht wie durch die Ungleichung verlangt ein Ergebnis, das größer oder gleich 9 ist. Somit ist es klar, dass alle Zahlen des grünen Bereichs die Ungleichung erfüllen; wir haben also die gesuchte Definitionsmenge ermittelt:

D=

Oder in der Intervallschreibweise:

D=

Oder etwas eleganter:

D=ℝ∖

Diese Schreibweise muss du nicht unbedingt selbst verwenden, solltest sie aber zumindest verstehen, da sie von vielen Lehrern bevorzugt benützt wird. Diese Schreibweise wird immer dann gerne verwendet, wenn die Lösungs- oder Definitionsmenge aus zwei getrennten Bereichen besteht, wie in unserem Beispiel.

Es ist einfacher anzugeben, dass alle reellen Zahlen ohne den Zahlen von ausgeschlossen -3 bis ausgeschlossen 3 die Definitionsmenge bilden. In einfacheren Worten: Man darf alle Zahlen aus ℝ einsetzen ohne -3, ohne 3 und ohne den Zahlenbereich dazwischen.

Oder anders herum gesagt: Die Zahlen, die größer als -3 aber auch kleiner als 3 sind, dürfen nicht eingesetzt werden, weil dann der Radikand negativ werden würde.

Lösung: D=

Oder in der Intervallschreibweise:

D=

Wir haben also wieder eine quadratische Ungleichung zu lösen, wie im Beispiel e).

Da es wesentlich einfacher ist, lösen wir –wie schon im vorherigen Beispiel gezeigt- an Stelle der Ungleichung zuerst die quadratische Gleichung:

Wie im Beispiel e) bereits ausführlich erklärt, denken wir uns einen Zahlenstrahl und überprüfen, in welchem Bereich die Zahlen liegen, die die Ungleichung erfüllen.

Setzt man Zahlen aus dem lilafarbenen Bereich in die Ungleichung ein, stellt man fest, dass die Ungleichung erfüllt ist.

Zahlen aus den beiden grünen Bereichen führen dagegen zu falschen Aussagen; sie erfüllen die Ungleichung nicht. Man darf also nur Zahlen von einschließlich -4 bis 4 in den gegebenen Term einsetzen; nur dann wird der Radikand nicht negativ.

Die Zahlen -4 und 4 dürfen gerade noch eingesetzt werden, weil sich dann die Wurzel aus Null ergibt und das ja definiert ist mit .

Der Radikand darf also gleich Null sein und deshalb können auch die Zahlen -4 und 4 noch eingesetzt werden. Die Grenzen sind deswegen in der Definitionsmenge eingeschlossen und es gilt:

D=

Oder in derIntervallschreibweise:

D=

Da hier kein zweigeteilter Bereich vorliegt, gibt es keine weitere Schreibweise wie im Beispiel e). Schreibweisen wie ℝ∖ oder ℝ∖ machen nur Sinn, wenn ein ganzer Zahlenbereich nicht verwendet werden darf, also ausgeschlossen werden soll.

Lösung: D=

Oder in Intervallschreibweise:

D=

Oder etwas eleganter:

D=ℝ∖

Erklärung:

Da die Wurzel hier im Nenner auftritt, muss beachtet werden, dass der Radikand auch nicht gleich Null werden darf. Die Wurzel aus Null ergibt bekanntlich Null; die Division durch Null ist aber nicht definiert. Daher gilt hier –wie im Beispiel c) – anstatt Radikand größer oder gleich Null, dass der Radikand größer als Null sein muss. Deshalb ergibt sich folgende (leider wieder quadratische) Ungleichung:

Zur Vereinfachung lösen wir wieder zuerst die quadratische Gleichung:

Da irrational ist, lässt sich die Wurzel nicht ziehen. Um nun die Zahlen zu finden, welche die Ungleichung erfüllen, bedienen wir uns wieder der Vorstellung eines Zahlenstrahls mit den eingetragenen Zahlen und .

Durch zur Probe eingesetzte Zahlen aus den verschiedenfarbigen Bereichen, erkennt man schnell, dass nur Zahlen aus den beiden grünen Bereichen die Ungleichung erfüllen. ( Z.B. ergibt oder also eine wahre Aussage, jedoch aber also offensichtlich einen Widerspruch zur Ungleichung ) D.h. es dürfen entweder Zahlen für x eingesetzt werden, die kleiner als sind, oder größer als .

Als Doppelungleichung geschrieben sieht das dann so aus:

Oder in der Intervallschreibweise:

Oder wir geben an, welche Zahlen nicht verwendet werden dürfen: D.h. es können alle Zahlen für x eingesetzt werden, außer die Zahlen von bis . Die Grenzen und müssen ausgeschlossen werden, da sonst der Nenner gleich Null werden würde.

Anstatt kann natürlich auch D= geschrieben werden, beides ist gleichbedeutend; es soll ja nur angegeben werden, welche Werte man für x einsetzen darf. Die Definitionsmenge enthält schließlich alle Werte aus der Grundmenge G, die für x eingesetzt werden können.

(nur für Schüler, die die binomischen Formeln bereits gelernt haben)

Lösung: D=G=ℝ

Erklärung:

Da die Wurzel nicht im Nenner steht, gilt nur die Bedingung, dass der Radikand größer oder gleich Null sein muss.

Allerdings stellt sich nun ein neues Problem: Wie löst man eine Ungleichung, die neben einem auch ein (ohne Quadrat) und eine Konstante (d.h. eine Zahl ohne ) enthält? Hier hilft momentan nur eine Umformung mit Hilfe der zweiten binomischen Formel

Wegen der geraden Potenz kann die Klammer gar nicht negativ werden, egal was man für x einsetzt. Daher gilt: D=G=ℝ

i)

(nur für Schüler, die die binomischen Formeln bereits gelernt haben)

Lösung: D=ℝ∖

Erklärung:

Da die Wurzel bei dieser Aufgabe im Nenner steht, darf der Radikand nicht gleich Null und auch nicht negativ sein:

Auch bei dieser Ungleichung hilft wieder nur die Umformung mit Hilfe einer binomischen Formel. Hier benötigen wir die erste binomische Formel:

Wegen der geraden Potenz kann die Klammer nicht negativ werden, allerdings würde sich in der Klammer Null ergeben, wenn für eingesetzt werden würde. D.h. nur für wäre die Ungleichung nicht erfüllt, deshalb dürfen alle reellen Zahlen außer in den Term eingesetzt werden.