Irrationale Zahlen, die Menge der reellen Zahlen und reinquadratische Gleichungen in der Menge ℝ
π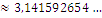
π∉ℚ π∈ℝ
π∉ℚ π∈ℝ!
Wiederholung:
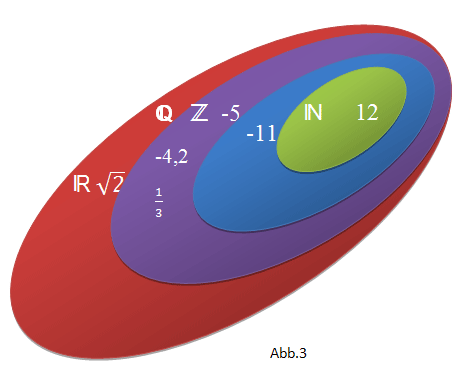
ℕ: Natürliche Zahlen (ohne 0)
ℕ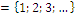
: Natürliche Zahlen (einschließlich 0) 
ℤ: Ganze Zahlen ℤ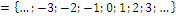
ℚ: Rationale Zahlen, also alle Brüche, endliche und periodische Dezimalzahlen (Nicht zu ℚ gehören z.B. Wurzeln, die nicht aufgehen, oder unendliche nicht periodische Dezimalzahlen)
ℝ: Reelle Zahlen, also alle rationalen und irrationalen Zahlen, d.h. alle dir momentan bekannten Zahlen
ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ
In Worten: ℕ ist Teilmenge von ℤ (d.h. ℕ liegt in ℤ)
ℤ ist wiederum eine Teilmenge von ℚ (d.h. ℤ liegt in ℚ)
ℚ ist wiederum eine Teilmenge von ℝ (d.h. ℚ liegt in ℝ)
ℤ ∖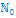 
= 
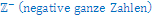
= ℚ ∖ ℤ = B (Brüche, periodische und endliche Dezimalzahlen)
ℝ ∖ ℚ = I (Irrationale Zahlen)
Alle in Rot geschriebenen Zeichen sollen vom Schüler im Programm angeklickt werden können, damit er dann die folgenden Zeichenerklärungen bekommt:
Aufgabenbeispiele:
Bsp.1: Sind folgende Aussagen wahr (w) oder falsch (f)?
 ∉ℚ |
(w)
|
kann man nicht ziehen, die Wurzel geht nicht auf, da 3 keine Quadratzahl ist. lässt sich daher nicht als endliche oder periodische Dezimalzahl schreiben. Deshalb ist irrational und gehört nicht zu ℚ. Also ist die Aussage wahr! |
|
∈ℝ |
(w)
|
ℝ ist die größte Zahlenmenge, die dir (momentan) zur Verfügung steht. Zu den reellen Zahlen ℝ gehören alle dir jetzt bekannten Zahlen. Daher gehört natürlich auch
dazu und die Aussage ist wahr! |
|
∉ℝ∖ℚ |
(f)
|
ℝ∖ℚ (in Worten: ℝ ohne ℚ) beschreibt die Menge der irrationalen Zahlen
 , welche in Abb.3 rot dargestellt ist. ist jedoch irrational, gehört also zu ℝ∖ℚ! Die Aussage ist falsch! |
 ∉ℚ |
(f)
|
Die Wurzel aus 25 lässt sich ziehen, da 25 eine Quadratzahl ist:
 Die Zahl 5 ist eine natürliche Zahl und gehört auch zur Menge ℚ. Deshalb ist die Aussage falsch!
|
 ∈ℚ |
(w)
|
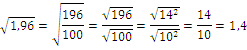 Da 1,4 eine endliche Dezimalzahl ist, gehört sie auch zur Menge der rationalen Zahlen ℚ. Die Aussage ist wahr!
|
 ∈ℤ |
(w)
|
 Da das Ergebnis -13 eine ganze Zahl ist, gehört es zur Menge ℤ. Die Aussage ist wahr!
|
|
19,14747474747…
∉ℝ∖ℚ
|
(w)
|
Anstelle von 19,14747474747… kann man auch 19,1
 schreiben, d.h. es handelt sich um eine gemischtperiodische Zahl. Alle periodischen Dezimalzahlen gehören bekanntlich zu den rationalen Zahlen ℚ und nicht zu den irrationalen Zahlen . Eine andere Schreibweise für I ist ℝ∖ℚ. (Vergleiche auch Abb.3: Die Zahl 19,1 liegt im lilafarbenen Bereich und nicht im roten Bereich.) Daher ist die Aussage "die Zahl 19,1 gehört nicht zu den irrationalen Zahlen" wahr! |
|
19,10100100010000…∈ℚ
|
(f)
|
Diese Zahl ist nicht periodisch, auch wenn man das im ersten Moment glauben könnte. Deshalb handelt es sich bei ihr um eine irrationale Zahl, sie gehört also nicht zur Menge ℚ. Die Aussage ist falsch!
|
|
19,123456789101112…∉ℚ
|
(w)
|
Es handelt sich um eine nichtperiodische unendliche Dezimalzahl, also um eine irrationale Zahl. Sie gehört natürlich nicht zur Menge der rationalen Zahlen ℚ. Die Aussage ist wahr!
|
