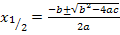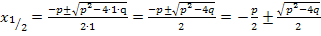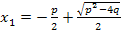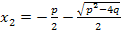Satz von Vieta

I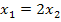         

II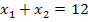         

III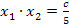       

Es liegt nun ein Gleichungssystem mit drei Gleichungen für die drei Unbekannten , und c vor. Erfreulicherweise kommt in den Gleichungen I und II die Unbekannte c gar nicht vor, sondern nur und . Gleichung I ist auch schon nach aufgelöst, so dass I direkt in II eingesetzt werden kann:

I in II: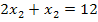

3 |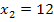

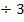
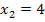
Sehr schön! Jetzt wissen wir schon ´mal . Das setzen wir in I (oder II) ein und erhalten sofort :

in I:

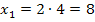
Wunderbar! Nun wissen wir auch, was ist. Es fehlt nur noch c und das können wir berechnen, indem wir und in III einsetzen:

und in III: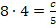         

|

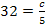
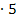
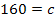
Damit ist die Aufgabe gelöst. Es gilt:

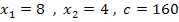
Die Aufgabe ist somit eindeutig lösbar. Fertig!

Du konntest hoffentlich an den gezeigten Beispielen erkennen, bei welchen Aufgaben der Satz von Vieta wirklich eine Hilfe darstellt.

So, nun soll für den daran interessierten Schüler zum Abschluss dieses Kapitels noch der Beweis des Satzes von Vieta vorgeführt werden. (Wenn es dich nicht interessiert, kannst du auch ohne schlechtes Gewissen den letzten Teil dieses Kapitels weglassen. Das Wichtigste zum Satz von Vieta hast du bereits erfahren.)

Beweis des Satzes von Vieta:

Zu Zeigen:

Für die Lösungen und einer normierten quadratischen Gleichung 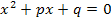gilt:

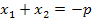
und 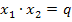     für p, q ℝ   Voraussetzung:D =

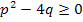
Wir gehen von der allgemeinen normierten Form einer quadratischen Gleichung aus und berechnen mit der Mitternachtsformel ihre Lösungen. Vorausgesetzt wird dabei, dass die Gleichung überhaupt lösbar ist, also dass die Diskriminante D größer oder gleich Null ist. Interessant ist, dass der Satz von Vieta auch dann noch gilt, wenn die beiden Lösungen und zu einer einzigen Lösung zusammenfallen, also wenn gilt: 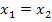, da D = 0

Im Regelfall stellen und jedoch zwei verschiedene Lösungen der quadratischen Gleichung 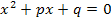dar. Für die Diskriminante D gilt dabei:D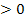

Vermutlich bist du es eher gewohnt mit der allgemeinen quadratischen Gleichung in der nicht-normierten Form 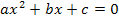zu arbeiten. Deshalb bleiben wir zuerst noch bei den Bezeichnungen a, b und c. Damit du leichter erkennen kannst, was in der normierten Form  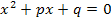den Koeffizienten a, b und c der allgemeinen Mitternachtsformel bezüglich 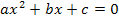entspricht, das Ganze noch einmal in verschiedenen Farben dargestellt:

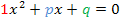
Wir berechnen nun die Lösungen und der normierten quadratischen Gleichung in Abhängigkeit von p und q.

---