Satz von Vieta
Laut Satz von Vieta gilt: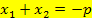 
und 
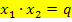
In unserem Fall also: 
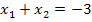
und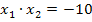 
Wir überlegen uns nun, welche Zahlen 
und 
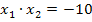die Gleichung erfüllen. Da kämen beispielsweise die Zahlenpaare 1 und -10 oder auch -1 und 10 in Frage. Genauso kommen jedoch auch die Zahlenpaare 2 und -5 oder mit umgedrehten Vorzeichen -2 und 5 in Frage. Alle diese Zahlenpaare ergeben jeweils mit einander multipliziert -10.
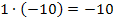
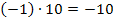
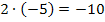
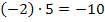
Jetzt kommt wieder die andere Bedingung 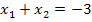ins Spiel. Die beiden Lösungen müssen also addiert -3 ergeben. Bei manchen Zahlenpaaren sieht man schon auf den ersten Blick, dass das nicht der Fall ist. Diese Zahlenpaare kannst du dann gleich wieder vergessen. Das ist zum Beispiel bei 1 und -10 oder auch bei -1 und 10 so.
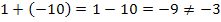
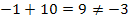
Die letzten beiden Zeilen brauchst du gar nicht hinschreiben;das mach man alles bloßim Kopf.
Das einzige unserer Zahlenpaare von oben, das auch die Bedingung 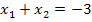erfüllt, ist das Paar 2 und -5, denn es gilt:
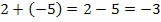(Sehr schön, das passt! Wir haben die Lösungen gefunden!)
Die Lösungen der Gleichung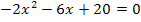 
sind deshalb: 
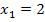und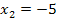 
Damit ist die Aufgabe gelöst. Mit ein wenig Übung sieht man die Lösungen vieler gemischtquadratischer Gleichungen, wenn sie normiert vorliegen, ganz schnell. Das hängt natürlich sehr von den vorkommenden Zahlen ab. Sind p und q beispielsweise Brüche oder Dezimalzahlen macht es keinen Sinn mit dem Satz von Vieta die Gleichung lösen zu wollen. Man berechnet dann die Lösungen besser mit der Mitternachtsformel.
Nun gibt es jedoch auch Aufgaben, bei denen eine der beiden Lösungen oder und einer der Koeffizienten p oder q gegeben ist, und die zweite Lösung und der andere Koeffizient einer normierten quadratischen Gleichung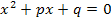 
gesucht ist. Solche Aufgaben löst man am besten wirklich immer mit dem Satz von Vieta. Schauen wir uns doch auch dazu einige Beispiele an.
3. Bsp.:
Von einer normierten quadratischen Gleichung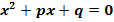 
ist eine der Lösungen 
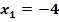und der Koeffizient p = 6 bekannt. Ermittle die zweite Lösung 
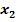und den Koeffizienten q der Gleichung!
Lösung:
Laut Satz von Vieta gilt: 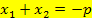und
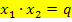
In unserem Fall also: 
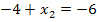
und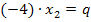 
Die erste Gleichung enthält nur die Unbekannte ;man kann sie einfach nach umformen. Danach setzen wir das Ergebnis von in die zweite Gleichung ein und lösen dies nach der verbleibenden Unbekannten q auf. Los geht´s!
| 
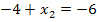
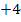
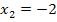
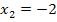eingesetzt in 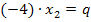ergibt: 
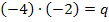
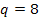
Damit ist die Aufgabe schon gelöst: ,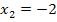
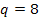
4. Bsp.:
Von einer quadratischen Gleichung der Form 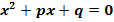sind die beiden Lösungen 
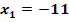und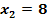 
bekannt. Welche Werte haben dann p und q?
Lösung:
Mit dem Satz von Vieta lässt sich diese Aufgabe ganz schnell lösen.
