Satz von Vieta
Da kämen beispielsweise die Zahlenpaare 1 und -12 oder auch -1 und 12 in Frage. Genauso kommen jedoch auch die Zahlenpaare 2 und -6 oder mit umgedrehten Vorzeichen -2 und 6 in Frage. Aber auch 3 und -4 oder wieder mit umgekehrten Vorzeichen -3 und 4. Alle diese Zahlenpaare ergeben jeweils mit einander multipliziert -12.
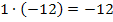
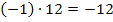
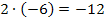
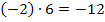
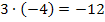
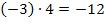
Puh, das sind aber viele mögliche Kandidaten für unsere gesuchten Lösungen 
und 
! Du musst sie auch nicht alle aufschreiben, wenn du selber rechnest. Das wurde nur hier gemacht, damit du die Überlegungen besser nachvollziehen kannst. Jetzt kommt wieder die andere Bedingung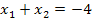 
ins Spiel. Die beiden Lösungen müssen also addiert -4 ergeben. Bei manchen Zahlenpaaren sieht man schon auf den ersten Blick, dass das nicht der Fall ist. Diese Zahlenpaare kannst du dann gleich wieder vergessen. Das ist zum Beispiel bei 1 und -12 oder auch bei -1 und 12 so.
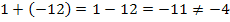
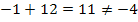
Das einzige unserer Zahlenpaare von oben, das auch die Bedingung 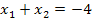erfüllt, ist das Paar 2 und -6, denn es gilt:
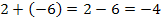(Super! Das passt! Wir haben die Lösungen gefunden!)
Die Lösungen der Gleichung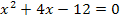 
sind deshalb: 
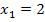und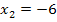 
Sobald man das passende Paar gefunden hat, kann man die restlichen Zahlenpaare von oben vergessen. Sie würden sowieso nicht stimmen. Es gibt schließlich maximal ein Zahlenpaar und , welches passt und somit die Lösungen der quadratischen Gleichung darstellt. Du könntest jetzt auch jeweils noch die Probe mit den beiden Lösungen 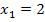und 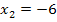machen. Wir sparen uns diese Rechnungen, weil du sie sicher alleine rechnen kannst. Die Vorgehensweise bei der Probe wurde ja schon in Teilaufgabe a.) gezeigt. Es sind hier nur andere Zahlen, doch sonst ist alles gleich.
zu c.)
Im Unterschied zu den vorherigen Teilaufgaben ist die Gleichung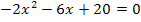 
noch nicht normiert. Vor 
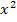steht ja noch die Zahl -2. In der vorliegenden Form lässt sich nicht sofort ablesen, was p bzw. q entspricht. Wir müssen die Gleichung daher vorweg normieren, also so umformen, dass keine Zahl mehr vor 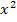vorkommt. Deshalb müssen wir die ganze Gleichung durch die Zahl -2 dividieren, d.h. es muss jeder Faktor der Gleichung einzeln durch -2 geteilt werden! Achte dabei besonders auf die Vorzeichen! Bei der Division durch eine negative Zahl drehen sich bekanntlich alle Vorzeichen um.
| 
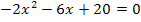
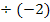
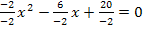
(Diesen Zwischenschritt musst du natürlich nicht hinschreiben!)
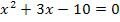
So, nun liegt die Gleichung in ihrer normierten Form vor und wir können p und q ablesen.
p = 3 , q = -10
Ab jetzt geht es genauso wie schon in den vorherigen Teilaufgaben erklärt weiter.
