Satz von Vieta
Also gilt hier:p = -8 , q = 7
Laut Satz von Vieta gilt für die gesuchten Lösungen 
und 
einer quadratischen Gleichung der Form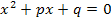 
: 
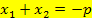
und 
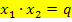
In unserem Fall also: 
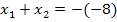und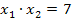 
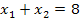
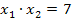
Wir überlegen uns nun, welche Zahlen und die Gleichung 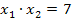erfüllen. Da kämen beispielsweise die Zahlenpaare 1 und 7 oder auch -1 und -7 in Frage. (Wir probieren nur ganze Zahlen aus, keine Dezimalbrüche etc., denn das wäre zu kompliziert.) Sowohl 
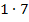als auch 
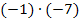ergibt 7. Welches Zahlenpaar stellt nun unsere Lösungen und dar? Um diese Frage zu beantworten, brauchen wir die andere Bedingung, nämlich 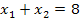. Wir testen deshalb einfach, ob 1 und 7 addiert 8 ergibt oder doch -1 und -7 diese Bedingung erfüllt. Man sieht natürlich sofort:
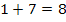(Ja, super! Das stimmt!)
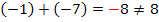(Stimmt nicht, wegen dem Minus-Zeichen!)
Das Zahlenpaar 1 und 7 erfüllt also die beiden Bedingungen 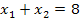und 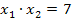. Somit sind die gesuchten Lösungen der quadratischen Gleichung 
:
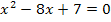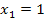und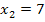 
. Fertig!
Falls du der Sache noch nicht so ganz traust, kannst du auch noch die Probe machen. Dazu setzt du hier einmal die Zahl 1 für jedes vorkommende x in die Gleichung ein;es muss sich Null ergeben, damit die Gleichung erfüllt ist. Genauso verfährt man dann mit der zweiten Lösung. Man setzt also für jedes x die Zahl 7 ein und schaut, ob sich Null ergibt.
Probe:
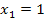in 
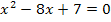
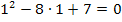
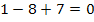
0 = 0 (Wahr)
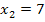in 
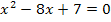
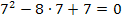
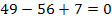
0 = 0 (Wahr)
Für die Zahlen 1 als auch 7 ist die Gleichung offensichtlich erfüllt; 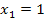und 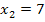sind wirklich Lösungen der Gleichung 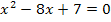. Dass es neben diesen beiden Lösungen keine weiteren Lösungen geben kann, wird klar, wenn man sich überlegt, dass eine quadratische Gleichung höchstens zwei Lösungen besitzt. Daher kann es keine dritte Lösung geben. Wir haben mit 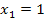und 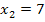alle denkbaren Lösungen ermittelt.
zu b.)
Jetzt noch einmal fast das Gleiche, nur eben mit anderen Zahlen. Allerdings wird es hier etwas aufwendiger. Wir sollen die Lösungen der Gleichung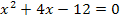 
ermitteln. Die Gleichung ist schon normiert, also lassen sich p und q sofort ablesen:
p = 4 , q = -12
Laut Satz von Vieta gilt: 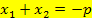und
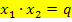
In unserem Fall also: 
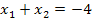
und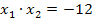 
Wir überlegen uns nun, welche Zahlen und die Gleichung 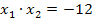erfüllen.
