Satz von Vieta

Wie bei der Einführung in die quadratischen Gleichungen bereits erläutert, wird die normierte Form einer quadratischen Gleichung allgemein in der Form 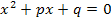geschrieben. In dieser Form lautet die Diskriminante dann eben D = .

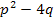Wozu kann man nun den Satz von Vieta brauchen? Mit seiner Hilfe lassen sich manchmal die beiden Lösungen und einer normierten, gemischtquadratischen Gleichung „erraten“. Mit „Erraten“ ist gemeint, dass man sich die Lösungen folgendermaßen überlegt:Man sucht nach zwei Zahlen 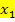und 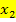, die miteinander multipliziert q, und addiert zusammen – p ergeben. Als Lösungen kommen dabei vor allem Teiler von q in Frage. Dieses Verfahren klappt natürlich nur dann gut, wenn die beiden Lösungen und ganze Zahlen sind.

Wenn man also auch nach einigem Probieren keine passenden Zahlen gefunden hat, heißt das noch lange nicht, dass es keine Lösungen gibt, sondern vielleicht nur, dass man sie nicht so leicht finden kann, weil und irgendwelche Dezimalzahlen oder irrationale Wurzeln sind. Du solltest dann nicht zu lange herumprobieren, sondern die Gleichung einfach mit der Mitternachtsformel lösen.

Den meisten Schülern fällt die Mitternachtsformel wesentlich leichter als die Verwendung des Satzes von Vieta. Viele Lehrer lösen jedoch gemischtquadratische Gleichungen schnell ´mal im Kopf;dabei benutzen sie eben meist den Satz von Vieta. Wie gesagt, musst du das nicht unbedingt können. Die Mitternachtsformel funktioniert schließlich auch. Nur in wenigen Fällen ist der Satz von Vieta wirklich wichtig für dich, da seine Anwendung die spezielle Aufgabe sehr erleichtert. In manchen Aufgaben ist die Anwendung des Satzes von Vieta natürlich auch ausdrücklich verlangt.

Jetzt möchtest du sicher endlich wissen, wie man den Satz von Vieta nun wirklich anwendet. Daher schauen wir uns ein paar Beispiele dazu an.

2. Bsp.:

Berechne mit dem Satz von Vieta die Lösungen der folgenden Gleichungen!

a.)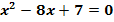

b.)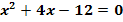

c.)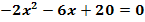

Lösung:

zu a.)

Wir suchen hier die Lösungen und der quadratischen Gleichung 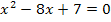.Diese Gleichungliegt bereits normiert vor, da vor 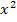nichts mehr steht. Da sich der Satz von Vieta immer auf die normierte Form einer quadratischen Gleichung 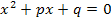bezieht, können wir direkt ablesen, was in diesem Fall p und was hier q entspricht. p ist immer die Zahl, die in der normierten quadratischen Gleichung vor x steht, einschließlich ihres Vorzeichens. q steht immer für die Zahl ohne x, ebenfalls einschließlich ihres Vorzeichens.

---