Satz von Vieta
Da bei dieser Gleichung der Koeffizient a gleich 1 ist, liegt die Gleichung bereits in normierter Form 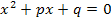 vor und wir können die Zahl vor x (in unserem Fall:7) an Stelle von b auch mit p und die Zahl ohne x (in unserem Fall:12) an Stelle von c auch mit q bezeichnen.
vor und wir können die Zahl vor x (in unserem Fall:7) an Stelle von b auch mit p und die Zahl ohne x (in unserem Fall:12) an Stelle von c auch mit q bezeichnen.
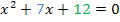
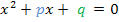
Es gilt daher:p = 7 , q = 12
Jetzt wollen wir ´mal schauen, ob es überhaupt stimmt, was oben über den Zusammenhang der Lösungen  und
und  mit den Koeffizienten p und q gesagt wurde. Also addieren wir die beiden Lösungen
mit den Koeffizienten p und q gesagt wurde. Also addieren wir die beiden Lösungen  und
und  , um zu überprüfen, ob dabei wirklich –p herauskommt. Des Weiteren multiplizieren wir die beiden Lösungen
, um zu überprüfen, ob dabei wirklich –p herauskommt. Des Weiteren multiplizieren wir die beiden Lösungen  und
und  miteinander, damit wir kontrollieren können, ob sich tatsächlich q ergibt.
miteinander, damit wir kontrollieren können, ob sich tatsächlich q ergibt.
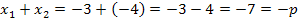 Das stimmt schon ´mal.
Das stimmt schon ´mal.
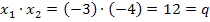
![]() Stimmt auch!
Stimmt auch!
Wir könnten das jetzt mit vielen verschiedenen Gleichungen der Form 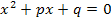 machen und würden dann feststellen, dass dieser Zusammenhang der Lösungen
machen und würden dann feststellen, dass dieser Zusammenhang der Lösungen  und
und  mit p und q wirklich immer gilt. Diese Arbeit ersparen wir uns aber besser und versuchen uns lieber später an einem allgemeinen Beweis. (Der Beweis des Satzes von Vieta kommt erst ganz am Schluss dieses Kapitels. Die meisten Schüler finden allgemeine Beweise eher verwirrend, als hilfreich, weil sie ziemlich schwierig sind. Da auch dieser Beweis nicht so ganz leicht ist, heben wir ihn uns einfach für später auf. Du wirst ihn auch in Prüfungen niemals selbst durchführen müssen! Insofern könntest du ihn mit gutem Gewissen übergehen. Für besonders interessierte Schüler soll jedoch auch der Beweis ausführlich erklärt werden. Siehe unten!) Nun wollen wir den oben beschriebenen Zusammenhang der Lösungen
mit p und q wirklich immer gilt. Diese Arbeit ersparen wir uns aber besser und versuchen uns lieber später an einem allgemeinen Beweis. (Der Beweis des Satzes von Vieta kommt erst ganz am Schluss dieses Kapitels. Die meisten Schüler finden allgemeine Beweise eher verwirrend, als hilfreich, weil sie ziemlich schwierig sind. Da auch dieser Beweis nicht so ganz leicht ist, heben wir ihn uns einfach für später auf. Du wirst ihn auch in Prüfungen niemals selbst durchführen müssen! Insofern könntest du ihn mit gutem Gewissen übergehen. Für besonders interessierte Schüler soll jedoch auch der Beweis ausführlich erklärt werden. Siehe unten!) Nun wollen wir den oben beschriebenen Zusammenhang der Lösungen  und
und  mit den Koeffizienten p und q aber erst einmal mathematisch korrekt niederschreiben.
mit den Koeffizienten p und q aber erst einmal mathematisch korrekt niederschreiben.
Mathematisch geschrieben sieht das dann folgendermaßen aus:
| Satz von Vieta:
Für die Lösungen
|
Anmerkung:
Damit der Satz von Vieta gelten kann, muss die quadratischen Gleichung 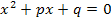 natürlich erst einmal lösbar sein. Genau dies drückt die Voraussetzung D =
natürlich erst einmal lösbar sein. Genau dies drückt die Voraussetzung D = 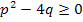 aus. Die Diskriminante D darf nicht negativ sein, damit es überhaupt Lösungen einer quadratischen Gleichung gibt, da die Diskriminante in der Mitternachtsformel unter der Wurzel steht, und aus negativen Zahlen bekanntlich keine Wurzel gezogen werden kann.
aus. Die Diskriminante D darf nicht negativ sein, damit es überhaupt Lösungen einer quadratischen Gleichung gibt, da die Diskriminante in der Mitternachtsformel unter der Wurzel steht, und aus negativen Zahlen bekanntlich keine Wurzel gezogen werden kann.
Du kennst sicher die Diskriminante der quadratischen Gleichung 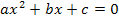 mit
mit 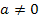 in der Form D =
in der Form D = 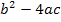 . Warum steht dann hier D =
. Warum steht dann hier D = 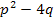 ? Der Satz von Vieta bezieht sich ja auf die normierte Form einer quadratischen Gleichung, also auf eine quadratische Gleichung, in der „keine“ Zahl vor
? Der Satz von Vieta bezieht sich ja auf die normierte Form einer quadratischen Gleichung, also auf eine quadratische Gleichung, in der „keine“ Zahl vor 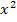 steht, genauer gesagt a = 1 gilt.
steht, genauer gesagt a = 1 gilt.

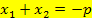 und
und 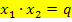 p, q
p, q  ℝ Voraussetzung: D =
ℝ Voraussetzung: D = 