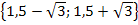Quadratische Ergänzung (zur Lösung gemischtquadratischer Gleichungen)
1. Variante
Ermittle durch quadratische Ergänzung die Lösungsmenge aller folgenden Gleichungen! G = ℝ
1. Bsp.:
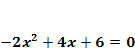
Lösung:
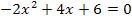
1. Schritt:a = -2 ausklammern![]()
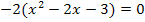 |
| 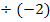
2. Schritt:Alles durch a dividieren![]()
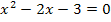
3. Schritt:Quadratische Ergänzung![]()
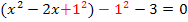
4. Schritt:Binomische Formel umformen 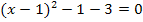
5. Schritt:Zusammenfassen soweit möglich 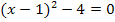
![]() |
| 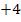
6. Schritt:Umstellen und Wurzelziehen 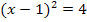
![]() |
| 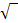
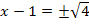
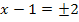
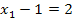 |
| 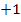
![]()
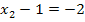 |
| 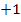
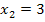
![]()
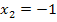
Die Lösungsmenge L lautet somit: L = 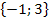
2. Bsp.:![]()
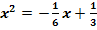
Lösung:
Wir bringen zuerst alles auf eine Seite der Gleichung, um die Gleichung in der von uns gewünschten Form 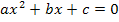 zu erhalten. Ob man dabei alles nach links oder alles nach rechts bringt ist an sich egal. In diesem Fall ist es jedoch geschickter alles auf die linke Seite der Gleichung zu bringen, weil dann vor
zu erhalten. Ob man dabei alles nach links oder alles nach rechts bringt ist an sich egal. In diesem Fall ist es jedoch geschickter alles auf die linke Seite der Gleichung zu bringen, weil dann vor 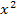 kein Minus-Zeichen zustehen kommt. Würde man
kein Minus-Zeichen zustehen kommt. Würde man 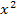 auf die rechte Seite der Gleichung bringen, stünde dort nämlich
auf die rechte Seite der Gleichung bringen, stünde dort nämlich 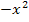 und dann müssten wir im nächsten Schritt eben dieses Minus-Zeichen, genauer gesagt die Zahl -1, ausklammern. Diesen Schritt können wir uns aber ersparen, wenn wir alles auf die linke Seite der Gleichung bringen. Dann ist a (= Zahl vor
und dann müssten wir im nächsten Schritt eben dieses Minus-Zeichen, genauer gesagt die Zahl -1, ausklammern. Diesen Schritt können wir uns aber ersparen, wenn wir alles auf die linke Seite der Gleichung bringen. Dann ist a (= Zahl vor 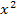 ) nämlich +1 und das Ausklammern von a entfällt.
) nämlich +1 und das Ausklammern von a entfällt.
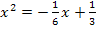
![]() |
| 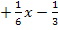
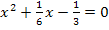
Nun können wir schon quadratisch ergänzen (vgl.:3. Schritt). Wegen a = 1 brauchen wir a hier ja nicht ausklammern. Daher entfallen die Schritte 1 und 2.
Hinweis:Ein Bruch wird halbiert, indem man entweder den Zähler halbiert (wenn dadurch keine Kommazahl im Zähler des Bruchs entsteht) oder indem man den Nenner verdoppelt. Den Bruch  halbiert man also durch Verdoppeln des Nenners, da eine Halbierung des Zählers zu der Dezimalzahl 0,5 führen würde und eine Kombination von Dezimalzahl (=Kommazahl) und Bruch wollen wir nicht haben. Die Hälfte von
halbiert man also durch Verdoppeln des Nenners, da eine Halbierung des Zählers zu der Dezimalzahl 0,5 führen würde und eine Kombination von Dezimalzahl (=Kommazahl) und Bruch wollen wir nicht haben. Die Hälfte von  ist somit
ist somit 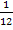 .
.
3. Schritt:Quadratische Ergänzung
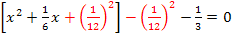
4. Schritt:Binomische Formel umformen
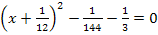
5. Schritt:Zusammenfassen soweit möglich
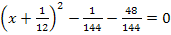
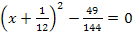
![]() |
| 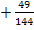
6. Schritt:Gleichung umstellen, Wurzelziehen und jeweils nach x auflösen
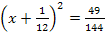 |
| 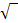
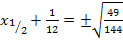
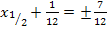
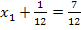
![]() |
| 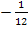
![]()
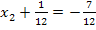
![]() |
| 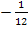
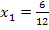
![]()
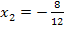
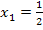
![]()
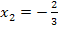
Die Lösungsmenge L über der Grundmenge G = ℝist damit: L = 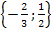
3. Bsp.:![]()
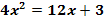
Lösung:
Zuerst bringen wir alles auf eine Seite der Gleichung. Ob man alles nach links oder nach rechts bringt, ist hier völlig egal. Wir entscheiden uns dazu, alles auf die linke Seite der Gleichung zu bringen.
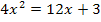 |
| 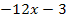
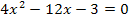
Nun können wir wieder nach unserem 6. Schritte-Plan vorgehen.
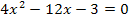
1. Schritt:a = 4 ausklammern![]()
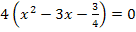 |
| 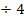
2. Schritt:Alles durch a dividieren![]()
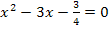
3. Schritt:Quadratische Ergänzung![]()
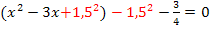
4. Schritt:Binomische Formel umformen 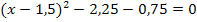
5. Schritt:Zusammenfassen soweit möglich 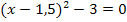
![]() |
| 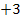
6. Schritt:Umstellen und Wurzelziehen 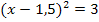
![]() |
| 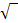
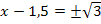
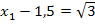 |
| 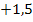
![]()
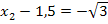 |
| 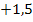
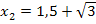
![]()
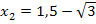
Die Lösungsmenge L lautet somit: L =