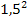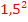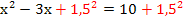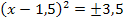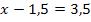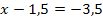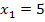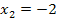Quadratische Ergänzung (zur Lösung gemischtquadratischer Gleichungen)
| Anleitung zur quadratischen Ergänzung
2. Variante |
Konkretes Beispiel |
Geg.: 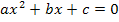 |
Geg.: 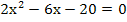 |
| 1. Schritt:a ausklammern
d.h. jeden Faktor einzeln durch a teilen |
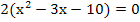 |
| 2. Schritt: Durch a auf beiden Seiten der Gleichung teilen | 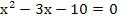 |
| 3. Schritt:Konstante (Zahl ohne x) auf die andere Seite bringen | 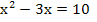 |
| 4. Schritt:Quadratisch ergänzen, um eine binomische Formel auf der linken Seite herzustellen
d.h. man nimmt die Zahl vor dem x (ohne Vorzeichen) halbiert und quadriert sie;das addiert man jeweils auf beiden Seiten der Gleichung, damit sich an der Gleichung insgesamt nichts ändert. (Man muss auf beiden Seiten + schreiben, da andernfalls auf der linken Seite keine binomische Formel entsteht. Weder die erste noch die zweite binomische Formel haben hinten ein Minus!) Zur Wiederholung: 1. Binom: 2. Binom: |
Die Zahl vor dem x (ohne Vorzeichen) ist hier 3
Halbiert Quadriert Auf beiden Seiten + So erhalten wir:
Auf der linken Seite der Gleichung steht hier die zweite binomische Formel, da vor 3x ein Minus steht. (Hätte vor 3x ein Plus gestanden, hätte sich die erste binomische Formel ergeben.) |
| 5. Schritt:Auf der linken Seite Binomische Formel umformen und auf der rechten Seite der Gleichung zusammenfassen so weit möglich | 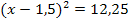
Ist dir dieser Schritt nicht klar, wiederhole bitte das Rechnen mit Binomischen Formeln! |
| 6. Schritt:Wurzel ziehen!
Achtung: Plus/Minus vor der Wurzel nicht vergessen! |

|
Weil die quadratische Ergänzung aus ziemlich vielen Einzelschritten besteht, schleichen sich relativ schnell verschiedenste Leichtsinnsfehler ein. Da hilft nur eines:Üben, Üben und noch ´mal Üben! Das kann dir niemand abnehmen. Damit du gleich noch ein paar Aufgaben zum Üben hast, kommen im Folgenden einige weitere Beispielaufgaben mit kompletter Lösung. Versuche sie jedoch zuerst alleine durchzurechnen und erst dann mit der Lösung zu vergleichen. Für jedes der folgenden Aufgabenbeispiele stehen beide Lösungsvarianten der quadratischen Ergänzung komplett durchgerechnet zur Verfügung. Du brauchst nur die für dich passende Variante auswählen.
Wähle nun die für dich passende Variante der quadratischen Ergänzung aus! Alle folgenden Beispiele werden dann mit diesem Lösungsweg gezeigt.

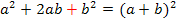
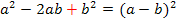
 1,5
1,5