Graphische Lösungsverfahren quadratischer Gleichungen

So erhält man die gesuchten Lösungen der quadratischen Gleichung 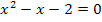. Sie lauten: 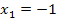und

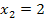
Damit kann die Lösungsmenge L angegeben werden:  L =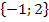

Warum entsprechen die x-Koordinaten der Schnittpunkte der Normalparabel y = und der Gerade y = 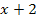überhaupt den Lösungen der quadratischen Gleichung 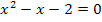? Das lässt sich leicht erklären:Um die Schnittpunkte zweier Funktionen zu berechnen, müssen die zwei Funktionsgleichungen zuerst gleichgesetzt und dann die entstandene Gleichung nach x aufgelöst werden. 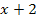Wollte man versuchen die Schnittpunkte der Normalparabel y = mit der Gerade y = rechnerisch zu ermitteln, müsste man also die Gleichung der Normalparabel mit der Gerade gleichsetzen. Es würde die folgende Gleichung entstehen:

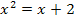
Diese ist äquivalent (gleich bedeutend) mit der quadratischen Gleichung 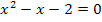. Jeweils  eine der beiden Gleichungen lässt sich schließlich durch eine einfache Umformung  in die andere überführen.

|

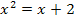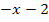
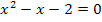
Daher sind die Zahlen, die die quadratische Gleichung 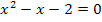erfüllen, auch die Zahlen, welche die Gleichung 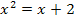erfüllen, also die x-Koordinaten der Schnittpunkte der Normalparabel y = und der Geraden y = 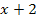.  Kennen wir die x-Koordinaten dieser Schnittpunkte, wissen wir somit die Lösungen unserer quadratischen Gleichung.

In diesem Beispiel gab es zwei Lösungen der quadratischen Gleichung. Wie du weißt ist das nicht immer der Fall. Schließlich schneidet nicht jede Gerade die Normalparabel y = in zwei Punkten. Wir haben ja bereits festgestellt, dass eine quadratische Gleichung entweder zwei Lösungen, genau eine oder gar keine Lösung besitzen kann. Daher wollen wir uns noch jeweils ein Beispiel für die anderen beiden Fälle anschauen.

5. Bsp.:

Gib die Lösungsmenge der Gleichung 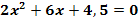an! (Graphische Lösung)

Lösung:

Wir gehen nach dem bei Methode 2 beschriebenen Verfahren vor. Wir lösen also erst einmal nach auf.

|

|

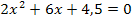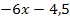
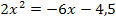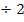
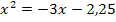
Dieselbe Gleichung wäre auch bei der Berechnung des gemeinsamen Punktes der Normalparabel y = und der Geraden y 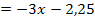entstanden. Daher zeichnet man die Graphen der Funktionen  y = und y 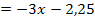in ein gemeinsames Koordinatensystem ein und lesen dann die x-Koordinate des gemeinsamen Punktes ab. (Hier existiert, wie du gleich selbst sehen wirst, nur eine Lösung.) Das kannst du gleich ´mal selbst ausprobieren. Achte darauf, dass du wirklich so genau wie möglich zeichnest, da sich Zeichenungenauigkeiten bei dieser Methode leider sehr stark auswirken! Am besten zeichnest du nicht nur ein, sondern mehrere Steigungsdreiecke, um die Gerade wirklich so genau wie möglich zu zeichnen. In deiner Zeichnung sollte die Gerade die Parabel berühren;sie sollte also Tangente an die Parabel sein. (Vergleiche Abbildung unten!

---