Graphische Lösungsverfahren quadratischer Gleichungen

Hier noch einmal das ganze Verfahren in Stichpunkten zusammengefasst:

Vorgehensweise bei der graphischen Lösung quadratischer Gleichungen (2.Methode)

·        Quadratische Gleichung nach 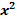auflösen

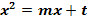
·        Linke Seite der Gleichung als Normalparabel y = 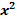betrachten

·        Rechte Seite der Gleichung als Gerade y = 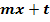ansehen

·        Normalparabel und Gerade in ein gemeinsames Koordinatensystem einzeichnen

·        x-Koordinaten der gemeinsamen Punkte (falls vorhanden) aus der Zeichnung ablesen

·        Das sind die gesuchten Lösungen der quadratischen Gleichung.

Zu kompliziert? Also schauen wir uns besser ´mal ein konkretes Beispiel an. Dann wird es hoffentlich klar, wie diese Methode funktioniert.

4. Bsp.:

Ermittle graphisch die Lösungsmenge der Gleichung !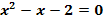

Lösung:

Wir gehen, wie soeben beschrieben vor. (Natürlich hätten wir auch die 1. Methode verwenden können, doch soll hier schließlich die 2. Methode vorgestellt werden.) Wir formen die Gleichung so um, dass alleine auf der linken Seite der Gleichung steht.

|

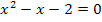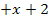
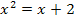
Nun sehen wir die linke Seite als Gleichung der Normalparabel y = und die rechte Seite der Gleichung als Gerade y = 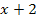an. Dann zeichnen wir die Normalparabel und die Gerade in ein gemeinsames Koordinatensystem ein.

Zur Erinnerung:Eine Gerade der Form y = mx + t kann mit Hilfe ihrer Steigung m und dem y-Achsenabschnitt t gezeichnet werden. Bei t schneidet die Gerade die y-Achse. Man geht also vom Ursprung t nach oben, wenn t positiv ist, bzw. t nach unten, wenn t negativ ist. Von dort ausgehend wird dann das Steigungsdreieck eingezeichnet. Dazu stellst du dir die Steigung m als Bruch vor und gehst den Nenner des Bruchs nach rechts und den Zähler nach oben, falls m positiv ist, bzw. nach unten, falls m negativ ist. Ausführlichere Erklärungen dazu findest du im Kapitel Lineare Funktionen / Geraden.

Die Parabel y = kann man ja ganz leicht mit Hilfe ihres Scheitels S(0|0) und einer Parabelschablone zeichnen. Die Gerade y = 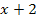zeichnet man mit Hilfe ihres y-Achsenabschnittes t = 2 und ihrer Steigung m = 1 = .

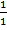Man geht in diesem Fall also vom Koordinatenursprung um 2 nach oben;dort schneidet die Gerade die y-Achse. Von da aus geht man 1 nach rechts und 1 nach oben (m ist ja positiv);so erhält man einen zweiten Geradenpunkt. Mit Hilfe dieser zwei Punkte lässt sich die Gerade zeichnen.

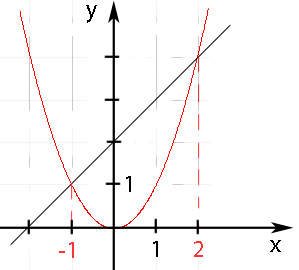
Abb.: Graph der Normalparabel y = und die Gerade y = 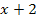mit ihren Schnittpunkten und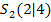

Nun braucht man nur noch die x-Koordinaten der Schnittpunkte von Parabel und Gerade aus der Zeichnung ablesen.

---