Graphische Lösungsverfahren quadratischer Gleichungen
h. wir multiplizieren mit der Zahl 2. ( Die Division durch einen Bruch entspricht, wie du sicher weißt, der Multiplikation mit dem Kehrbruch.)
| 
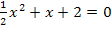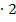
Die linke Seite der Gleichung stellen wir uns als Parabel f(x) =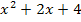 
vor. Um sie zeichnen zu können, berechnen wir beispielsweise mittels quadratischer Ergänzung ihren Scheitel S.
f(x) =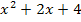
f(x) =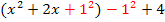 
f(x) =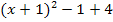 
f(x) =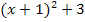 
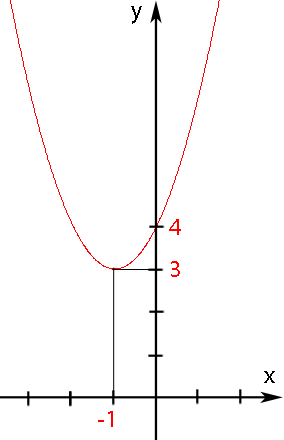
Nun liegt die Parabel in Scheitelform vor und wir können den Scheitel S(-1|3) bequem ablesen. Wenn du jetzt versuchst, dir vorzustellen, wie die Parabel im Koordinatensystem liegt, wirst du feststellen, dass sie gar keine Nullstellen haben kann. Der Scheitel S(-1|3) hat schließlich eine positive y-Koordinate und liegt somit oberhalb der x-Achse. Da die Parabel ja auch nach oben geöffnet ist, kann sie die x-Achse überhaupt nicht scshneiden! Du kannst sie natürlich auch einfach in ein Koordinatensystem einzeichnen, dann siehst du das ebenfalls. Die Lösungsmenge muss daher zwangsläufig leer sein, da schließlich keine Nullstellen (also Schnittpunkte mit der x-Achse) und somit keine Lösungen der quadratischen Gleichung existieren. Es gilt also:L = 
Damit du es dir besser vorstellen kannst, ist in der folgenden Abbildung der Graph der Funktion f(x) = 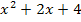dargestellt. Er schneidet die x-Achse nicht.
Abb.: Graph der Funktion f(x) =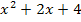
Schauen wir uns die drei gezeigten Beispiele noch einmal im Vergleich an. Im 1. Bsp. hatte die quadratische Gleichung zwei, im 2. Bsp. genau eine und im 3. Bsp. keine Lösung. Das sind alle Möglichkeiten, die es bezüglich der Anzahl der Lösungen einer quadratischen Gleichung gibt. Wie oben schon gesagt, hat eine quadratische Gleichung entweder zwei verschiedene, genau eine oder gar keine Lösung. Im Gegensatz dazu besitzt eine lineare Gleichung (d.h. eine ganz normale Gleichung ohne 
, z. B. 2x-6 = 0) immer genau eine Lösung.
Merke:Eine quadratische Gleichung kann auch zwei oder gar keine Lösungen haben, nicht nur eine! Das darfst du wirklich nie vergessen. Sehr oft kommt nämlich bei der rechnerischen Lösung einer quadratischen Gleichung, welche zwei Lösungen hat, bei Schülern, die das gerade erst lernen, der Fehler vor, dass zwar eine der beiden Lösungen korrekt ermittelt, aber die zweite völlig vergessen wird.
