Graphische Lösungsverfahren quadratischer Gleichungen
2. Bsp.:
Ermittle graphisch die Lösungsmenge der quadratischen Gleichung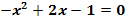 
!
Lösung:
Die Gleichung ist bereits nach Null aufgelöst. Die linke Seite der Gleichung kann man sich deshalb sofort, auch ohne weitere Umformungen, als nach unten geöffnete Normalparabel f(x) =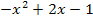 
vorstellen. Um sie zeichnen zu können, ermitteln wir zuerst ihren Scheitelpunkt. Dazu klammern wir zuerst a = -1 (also das Minuszeichen vor 
) aus, d.h. wir drehen in der Klammer alle Vorzeichen um. Normalerweise würde man dann quadratisch ergänzen, was hier jedoch unnötig ist, da nach dem Ausklammern sowieso schon die zweite biomische Formel vorliegt. Nun denkst du dir vielleicht, dass du alleine die binomische Formel nicht erkannt hättest. Das wäre auch nicht schlimm! Denn dann hättest du wie gewöhnlich quadratisch ergänzt, was zwar hier ein überflüssiger Rechenschritt gewesen wäre, aber trotzdem kein Fehler. Du würdest zum selben Ergebnis für den Scheitel kommen.
f(x) =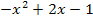
f(x) =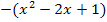 
Wir sparen uns die hier unnötige quadratische Ergänzung und formen die binomische Formel direkt um. So erhält man:
f(x) =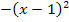 
Nun liegt schon die Scheitelform der Parabel vor. Falls dir hier irgendetwas – genau genommen die y-Koordinate des Scheitels – fehlt, denkst du dir einfach eine Null addiert. Dann sieht das ganze gleich viel mehr nach Scheitelform aus.
f(x) =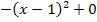 
Nun kannst du bestimmt die Scheitelkoordinaten ablesen. Sie lauten: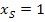 
und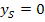 
Um die Lösung der quadratischen Gleichung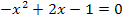 
graphisch zu ermitteln, müssen wir nur noch die Parabel f(x) in ein geeignetes Koordinatensystem einzeichnen. Das kannst du sicher alleine. Denk aber daran, dass es sich wegen a = -1 um eine nach unten geöffnete Normalparabel handelt! Den Scheitel S(1|0) kennen wir ja inzwischen. Damit lässt sich die Parabel mit Hilfe der Schablone leicht zeichnen.
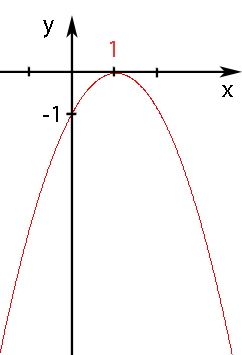
Abb.: Graph der Parabel f(x) =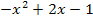
Da der Scheitelpunkt S(1|0) genau auf der x-Achse liegt, stellt er die einzige Nullstelle dar. Die Gleichung 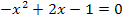hat daher nur eine einzige Lösung, nämlich x = 1.
Die Lösungsmenge lautet daher:L =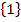 
3. Bsp.:
Gegeben ist die Gleichung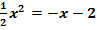 
. Ermittle graphisch ihre Lösungsmenge!
Lösung:
Die vorliegende quadratische Gleichung ist noch nicht nach Null aufgelöst. Daher bringen wir alles auf eine Seite der Gleichung. Damit sich positive Vorzeichen ergeben, entscheiden wir uns dafür, alles auf die linke Seite zu bringen.
| 
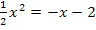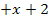
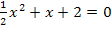
Wir dividieren nun die gesamte Gleichung durch den Faktor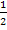 
, damit sich eine Normalparabel auf der linken Seite ergibt, d.
