Graphische Lösungsverfahren quadratischer Gleichungen
Nun kann natürlich auch einmal der Fall vorliegen, dass der Graph die x-Achse überhaupt nicht schneidet, dass also keine Nullstellen existieren. Dann hat die quadratische Gleichung gar keine Lösung:Die Lösungsmenge ist leer. Liegt der Scheitel der Parabel dagegen genau auf der x-Achse, so gibt es genau eine Nullstelle und somit auch genau eine Lösung der quadratischen Gleichung. Schneidet die Parabel die x-Achse allerdings in zwei Punkten, gibt es zwei Nullstellen und daher auch zwei Lösungen der quadratischen Gleichung. Du siehst, eine quadratische Gleichung kann entweder zwei, eine oder gar keine Lösung besitzen. Das hängt eben davon ab, wie oft die Parabel die x-Achse schneidet.
Damit das alles nicht nur graue Theorie bleibt, schauen wir uns ein paar Beispiele an.
1. Bsp.:
Ermittle graphisch die Lösungsmenge der Gleichung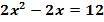 
!
Lösung:
Wir gehen genau wie oben beschrieben vor:
Zuerst bringen wir die Gleichung auf die Form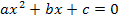 
. Wir müssen also nach Null auflösen. Dazu subtrahieren wir auf beiden Seiten der Gleichung die Zahl 12.
| 
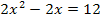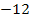
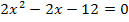
Nun liegt die Gleichung in der gewünschten Form 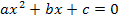vor. Die linke Seite der Gleichung könnte man sich nun bereits als Parabel y = 
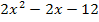vorstellen. Das wäre eine nach oben geöffnete Parabel, die wegen a = 2 schmäler als die Normalparabel wäre. Diese Parabel ließe sich nicht ohne Wertetabelle zeichnen. Angenehmer wäre es für uns, wenn eine Normalparabel vorliegen würde. Daher wenden wir unseren Trick an und dividieren durch a = 2, sodass danach die linke Seite der Gleichung eine Normalparabel bildet.
| 
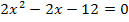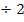
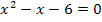
Die linke Seite der Gleichung bildet jetzt die Normalparabel f(x) =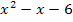 
. Da nun wegen a = 1 eine nach oben geöffnete Normalparabel vorliegt, brauchen wir nur noch die Scheitelkoordinaten ermitteln und können dann die Parabel ohne weitere Rechnung in ein Koordinatensystem einzeichnen. (Damit wir eine Normalparabel erhalten, haben wir ja vorher durch 2 geteilt. Hätten wir nicht durch 2 dividiert, sondern hätten direkt die Parabel y = 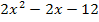zeichnen wollen, hätten wir, wie gesagt, eine Wertetabelle erstellen müssen, da es sich bei dieser Parabel um eine im Vergleich zur Normalparabel schmälere Parabel handelt. Das ist zwar auch nicht falsch, doch dauert dieses Vorgehen etwas länger und liefert vor allem ungenauere Ergebnisse, da sich hierbei Zeichenungenauigkeiten stärker auswirken.)
Wir müssen jetzt also den Scheitelpunkt der Parabel f(x) = 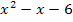berechnen.
