Graphische Lösungsverfahren quadratischer Gleichungen
Zur Erinnerung:Die Nullstellen einer Funktion sind die Schnittpunkte ihres Graphen mit der x – Achse. Da jeder Punkt der x – Achse die y – Koordinate y = 0 hat, muss auch für die Nullstellen y = 0 gelten. Weil nun aber die Schreibweise f(x) nichts anderes als y bedeutet, gilt bei den Nullstellen f(x) = 0. Das sagt wiederum nichts anderes aus, als dass man zur Berechnung der Nullstellen die Funktionsgleichung gleich Null setzen muss.
Wollten wir versuchen die Nullstellen unserer Parabel zu berechnen, müssten wir unsere Parabel f(x) =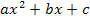 
gleich Null setzen. Dadurch würde dann die folgende Gleichung entstehen: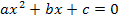 
Genau das ist aber doch die quadratische Gleichung, die wir ursprünglich lösen sollten! Nun müsste es dir einleuchten, warum die x-Koordinaten der Nullstellen unserer Parabel den Lösungen unserer Gleichung entsprechen.
Die zu lösende Gleichung entsteht praktisch durch die Nullstellenberechnung der Funktion f(x). Deshalb kann man die Lösungen der Gleichung 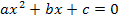als Nullstellen der Funktion f(x) = 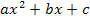auffassen.
Leider lassen sich bloßNormalparabeln, aber nicht breitere oder schmälere Parabeln, ganz schnell und trotzdem genau nur mit Hilfe ihres Scheitels und der Parabelschablone zeichnen. Eine Normalparabel liegt bekanntlich jedoch nur für a = 1 (nach oben geöffnet) bzw. a = -1 (nach unten geöffnet) vor. Für andere Werte von a müsste erst eine Wertetabelle erstellt werden, um die Parabel zeichnen zu können, da die Parabel dann ja breiter oder schmäler als die Normalparabel ist. Diese Arbeit kann man sich jedoch durch einen kleinen mathematischen Trick ersparen:Wir dividieren die ganze Gleichung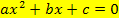 
durch den Faktor a, also durch die Zahl, die vor 
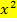steht, falls a 
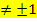ist. Dadurch entsteht die normierte Form der quadratischen Gleichung. (Vergleiche Einführung in die quadratischen Gleichungen) Wir erhalten also eine Gleichung, in der nun a = 1 ist. Die zugehörige Parabel ist nun genau wegen a = 1 eine nach oben geöffnete Normalparabel und die lässt sich natürlich viel besser zeichnen. Dann liest man noch die x-Koordinaten der Nullstellen der Normalparabel ab. Fertig!
Hier noch einmal das ganze Verfahren in Stichpunkten zusammengefasst:
| Vorgehensweise bei der graphischen Lösung quadratischer Gleichungen (1.Methode)
· Gleichung nach Null auflösen · Falls · Linke Seite der Gleichung als Parabel ansehen · Parabel in ein Koordinatensystem einzeichnen · x-Koordinaten der Nullstellen, falls vorhanden, ablesen · Das sind die gesuchten Lösungen der quadratischen Gleichung. |
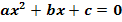
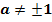: Division durch a
