Graphische Lösungsverfahren quadratischer Gleichungen

) Daher existiert hier, wie bereits erwähnt, genau eine Lösung. Wir lesen die x-Koordinate des Berührpunkts aus der Zeichnung ab. So erhalten wir die Lösung der quadratischen Gleichung:x = – 1,5

Die Lösungsmenge L lautet daher:L =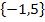

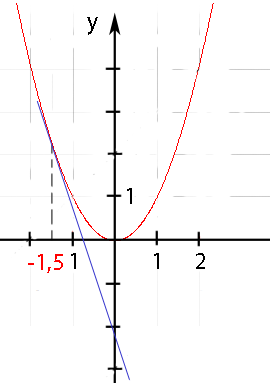
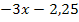Abb.: Graph der Normalparabel y = und die Gerade y = mit ihrem Berührpunkt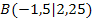

6. Bsp.:

Ermittle graphisch die Lösungsmenge der Gleichung !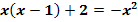

Lösung:

Zuerst multiplizieren wir die Klammer auf der linken Seite der Gleichung aus. Dann lösen wir wieder nach auf.

|

|

|

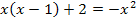
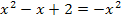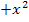
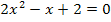
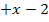
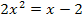
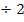
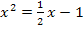
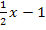Wir interpretieren die Gleichung wieder als den Versuch, die Normalparabel y = mit der Gerade y = zu schneiden. Wenn man die Parabel und die Gerade in ein gemeinsames Koordinatensystem einzeichnet, erkennt man sofort, dass sie sich überhaupt nicht schneiden. Die Lösungsmenge L ist deshalb leer:  L =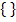

Hinweis zum Zeichnen der Gerade y = 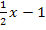:Gehe vom Ursprung aus um 1 nach unten (weil t = -1);dort schneidet die Gerade die y-Achse. Das ist dein erster Geradenpunkt. Von dort dann 2 nach rechts und 1 nach oben (weil m = 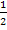);das ist dein zweiter Geradenpunkt. Will man ganz besonders genau zeichnen, von zweiten, gerade eingezeichneten Geradenpunkt ausgehend noch einmal 2 nach rechts und 1 nach oben;so erhält man einen dritten Geradenpunkt (zweites Steigungsdreieck). Das Einzeichnen des dritten Geradenpunkts ist hier nicht so wichtig, da man auch bei etwas ungenauerer Zeichnung sofort erkennt, dass es keine gemeinsamen Punkte von Parabel und Gerade gibt. (Das setzt natürlich voraus, dass auch die Parabel schon eingezeichnet ist.)

So, jetzt haben wir zu jedem Fall ein konkretes Beispiel für beide graphischen Lösungsverfahren von quadratischen Gleichungen gesehen. Du hast dabei sicher festgestellt, dass es manchmal nicht leicht ist, die Lösung wirklich exakt aus der Zeichnung abzulesen. Was macht man, wenn die Zahlen ´mal nicht „schön“ sind und daher die Schnittpunkte nicht auf den Kästchen deines Zeichenpapiers liegen? Da hilft nur Eines:Man muss die Lösung(en) rechnerisch ermitteln. Wenn du wissen willst, wie das funktioniert, gehe zu Rechnerische Lösungsverfahren quadratischer Gleichungen.

---