Einführung in die quadratischen Gleichungen

p und q mit der Lösung bzw. den Lösungen der quadratischen Gleichung (manchmal gibt es nämlich sogar zwei verschiedene Lösungen für x) zusammenhängen, werden wir später im entsprechenden Kapitel noch besprechen. Eine gegebene quadratische Gleichung zu normieren, ist auf jeden Fall nicht schwer;man muss nur durch a (die Zahl, die vor 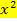steht) teilen. Danach  liegt die Gleichung in ihrer normierten Form vor.

2. Bsp.:

Wandle die folgenden quadratischen Gleichungen in ihre normierte Form um!

a.)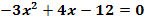

b.)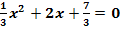

c.)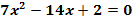

Lösung:

zu a.)

|

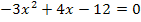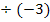
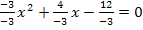
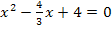
zu b.)

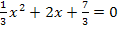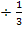| bzw. |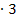

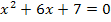
zu c.)

|

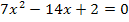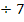
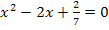
Das soll uns an Beispielen zum Normieren quadratischer Gleichungen genügen.

Manche Lehrer bringen jede quadratische Gleichung erst auf die normierte Form, um die Gleichung dann nach x aufzulösen. Diese Vorgehensweise ist vor allem in anderen Bundesländern gebräuchlich, jedoch selten in Bayern. Da sich diese website hauptsächlich am Schulstoff bayerischer Schulen orientiert, wird hier im Regelfall nicht erst in die normierte Form umgewandelt, sondern gleich mit der allgemeinen Form 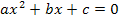gerechnet, da man sich dadurch einen Rechenschritt, nämlich die Division durch a, spart. In manchen Fällen ist es jedoch unerlässlich zuerst die normierte Form zu bilden, beispielsweise bei Aufgaben, die mit dem Satz von Vieta gelöst werden sollen. Darauf wird im entsprechenden Kapitel noch genauer eingegangen. Auch bei den graphischen Lösungsverfahren für quadratische Gleichungen empfiehlt es sich mit der normierten Form der jeweiligen Gleichung zu arbeiten. Du wirst die normierte Form daher noch öfter brauchen.

Reinquadratische und gemischtquadratische Gleichungen:

Wahrscheinlich kennst du bereits die sogenannten reinquadratischen Gleichungen, also Gleichungen vom Typ 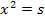(z.B. 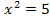). Vermutlich weißt du daher schon:Alle Gleichungen, die zwar 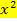aber kein x (ohne Quadrat) enthalten, nennt man reinquadratische Gleichungen.

Im Gegensatz dazu bezeichnet man Gleichungen, die 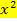und zugleich x (ohne Quadrat) enthalten, als gemischtquadratische Gleichungen. Außerdem kann auch noch eine Konstante, d.h. eine Zahl ohne x, vorkommen. Das muss aber nicht sein. (Dazu kommt unten gleich noch ein Beispiel.)

Die Gleichung 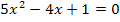ist z.B. gemischtquadratisch, da sie neben dem 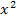auch ein x (ohne Quadrat) enthält. Die Gleichung 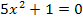ist dagegen reinquadratisch, weil sie nur 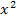aber kein x (ohne Quadrat) enthält. Die Gleichung 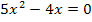ist wiederum gemischtquadratisch, weil sowohl 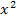als auch x (ohne Quadrat) vorkommt. Dass in dieser Gleichung keine Konstante (Zahl ohne x) vorkommt, ändert nichts daran. Die Gleichung ist trotzdem gemischtquadratisch.

---