Einführung in die quadratischen Gleichungen

So ist beispielsweise die Gleichung 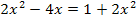nicht quadratisch, obwohl es im ersten Moment so scheint. Weil sich auf beiden Seiten der Gleichung der Ausdruck 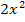befindet und der quadratische Term somit beim Umstellen der Gleichung letztendlich wegfällt, bleibt nach Subtraktion von 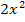auf beiden Seiten nur noch folgende Gleichung übrig: 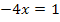Diese Gleichung ist offensichtlich nicht quadratisch;es ist ja gar kein 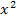mehr vorhanden! Ein anderes Beispiel einer nicht-quadratischen Gleichung, die aber trotzdem den Ausdruck  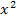enthält, ist die folgende Gleichung:  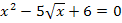Bei dieser Gleichung handelt es sich nämlich um eine Wurzelgleichung, da die Unbekannte x unter der Wurzel steht.

Merke dir also:Die Unbekannte darf bei einer quadratischen Gleichung keinesfalls unter einer Wurzel vorkommen und außerdem darf sich das Quadrat der Unbekannten nicht durch Umformungen der Gleichung wegheben.

Am besten schauen wir uns dies noch an einigen weiteren Beispielaufgaben an.

1. Bsp.:

Bei welchen der folgenden Gleichungen handelt es sich um quadratische Gleichungen? Gib außerdem bei den quadratischen Gleichungen an, was jeweils den Koeffizienten a, b und c entspricht! Vergleiche dazu mit der allgemeinen Form einer quadratischen Gleichung !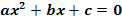

a.)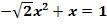

b.)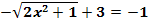

c.)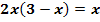

d.)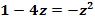

e.)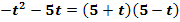

Lösung:

zu a.)

Die Gleichung 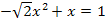ist quadratisch, da sie sich auf die Form 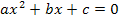mit 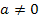bringen lässt:

|

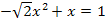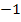
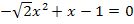
Dabei gilt: , ,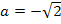

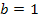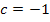
Dass bei dem Koeffizienten a eine Wurzel auftritt, ändert nichts daran, dass die Gleichung quadratisch ist. Nur die Unbekannte, hier also x, dürfte nicht unter der Wurzel stehen! Aber x ist hier ja nicht unter der Wurzel, nur die Zahl 2.

zu b.)

Die Gleichung 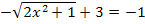enthält die Unbekannte x unter der Wurzel. Somit liegt hier eine Wurzelgleichung und keine quadratische Gleichung vor.

zu c.)

Die Gleichung 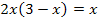müssen wir erst einmal vereinfachen, d.h. wir müssen ausmultiplizieren und dann umstellen.

|

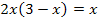
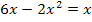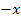
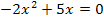
Man erkennt nun, dass hier wirklich eine quadratische Gleichung vorliegt. Die Konstante (Zahl ohne x) fehlt zwar, doch das bedeutet nur, dass c gleich Null ist. Daher gilt:

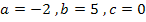
zu d.)

Die Unbekannte ist zwar in der Gleichung 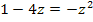nicht mehr x, sondern z, aber dennoch ist leicht zu erkennen, dass es sich hier um eine quadratische Gleichung handelt. Man könnte noch nach Null auflösen, um die Koeffizienten a, b und c besser ablesen zu können.

|

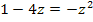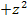
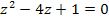
Nun erkennt man: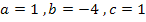

zu e.)

Bei der Gleichung 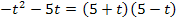muss man zuerst vereinfachen, bevor man sagen kann, ob es sich um eine quadratische Gleichung handelt oder nicht.

---