Diskriminante D

Jetzt fassen wir unsere Ergebnisse noch einmal zusammen:

Für 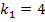und für 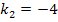: 1 Lösung

Für k 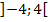: 2 Lösungen

Für k 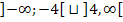: Keine Lösung

An diesem Beispiel konntest du sehen, wie unterschiedlich schwer Aufgaben mit Parameter sein können. Die Teilaufgabe c.) gehört dabei sicher zur schwierigsten Kategorie, die du in der 9. Klasse (Gymnasium) lösen können solltest. Wenn du mehr zu dem Thema quadratische Ungleichungen erfahren willst, gehe zu Quadratische Ungleichungen. Dort wird neben dem graphischen Verfahren auch ein rechnerischer Weg erklärt;dieser ist jedoch sicher nicht einfacher. Deshalb wurde in Teilaufgabe c.) das graphische Verfahren gewählt. Wer die quadratischen Ungleichungen auch ohne Hilfsparabel nur im Kopf lösen kann, darf dies natürlich auch machen. Allerdings besteht dabei die große Gefahr, dass man dabei den Fehler begeht, den negativen Zahlenbereich zu vergessen. Also große Vorsicht, wenn du das im Kopf erledigen willst! Das solltest du wirklich erst machen, wenn du sehr geübt bist im graphischen Lösungsverfahren für quadratische Ungleichungen. Dann kann man sich die Skizze mit der Hilfsparabel auch einfach denken und muss sie nicht mehr auf das Papier zeichnen.

Zum Schluss noch ein weiteres Beispiel mit Parameter. Keine Angst! Es ist nicht ganz so schwer wie das Letzte. Hier kommt keine Ungleichung vor, doch interessant ist es aus anderem Grund. Schau es dir einfach an und versuche es alleine durchzurechnen.

3. Bsp.:

Für welche Werte von t hat die Gleichung 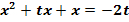genau eine Lösung?

Lösung:

Zuerst müssen wir die Gleichung nach Null auflösen. Wir brauchen sie schließlich in der Form 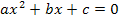, damit wir ablesen können, was a, b und c entspricht.

|

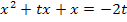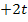
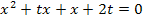
Nun stehen wir vor dem Problem, wie man denn tx und x zusammenfasst. Ganz einfach:Wir klammern das x einfach aus diesen beiden, aber wirklich nur aus diesen beiden Faktoren aus.

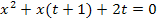
Jetzt drehen wir noch die Reihenfolge von x und der Klammer um.

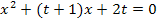
Somit kann man gut erkennen, was a, b und c entspricht.

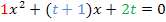
Da die Gleichung genau eine Lösung besitzen soll, muss gelten:D = 0

Wir berechnen daher die Diskriminante D in Abhängigkeit von t, also ohne etwas Konkretes für t einzusetzen, und setzen D anschließend gleich Null. Dann muss man nur noch nach t auflösen.

D =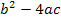

D =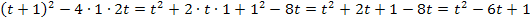

Anmerkung:Um die Klammer zu quadrieren wurde die erste Binomische Formelverwendet.

D = 0   

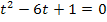
Nun liegt aber schon wieder eine (neue) gemischtquadratische Gleichung vor.

---