Diskriminante D
So erkennst du sicher, dass es sich um eine nach unten geöffnete Normalparabel handelt. Die Nullstellen dieser Parabel würden sich berechnen lassen, indem man 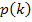 gleich Null setzt. So entstünde die Gleichung
gleich Null setzt. So entstünde die Gleichung 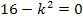 . Eben diese Gleichung haben wir bereits beim 1. Fall gelöst. Es ergab sich
. Eben diese Gleichung haben wir bereits beim 1. Fall gelöst. Es ergab sich 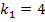 und
und 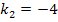 . Dort hat die Parabel also ihre Nullstellen. Mit diesem Wissen können wir die Parabel nun skizzieren, denn die x-Koordinate des Scheitels muss dabei natürlich in der Mitte der beiden Nullstellen liegen:
. Dort hat die Parabel also ihre Nullstellen. Mit diesem Wissen können wir die Parabel nun skizzieren, denn die x-Koordinate des Scheitels muss dabei natürlich in der Mitte der beiden Nullstellen liegen: 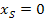 Die y-Koordinate des Scheitels erhält man durch Einsetzen von
Die y-Koordinate des Scheitels erhält man durch Einsetzen von 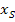 in die Parabelgleichung:
in die Parabelgleichung: 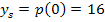
Hinweis:Eigentlich kommt es bei der benötigten Skizze gar nicht darauf an, in welcher Höhe der Scheitel liegt und wie breit die Parabel ist. Entscheidend ist vielmehr, ob die Parabel nach oben oder nach unten geöffnet ist, und wo die Nullstellen liegen. Es ist daher eine grobe Skizze von  völlig ausreichend. Der Scheitel müsste eigentlich gar nicht vorher berechnet werden. Weil jedoch die Nullstellen für die Skizze benötigt werden, rechnet man immer vorher als 1. Fall D = 0. Damit hat man die Nullstellen der Hilfsparabel schon berechnet.
völlig ausreichend. Der Scheitel müsste eigentlich gar nicht vorher berechnet werden. Weil jedoch die Nullstellen für die Skizze benötigt werden, rechnet man immer vorher als 1. Fall D = 0. Damit hat man die Nullstellen der Hilfsparabel schon berechnet.
Merke:Kommt bei einer Fallunterscheidung der Parameter zum Quadrat vor, beginnt man immer mit dem Fall D = 0. Somit hat man die Nullstellen der Hilfsparabel, die man zum Lösen der quadratischen Ungleichungen beim 2. und 3. Fall braucht, bereits berechnet.
Wir skizzieren nun die Hilfsfunktion 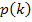 mit Hilfe ihrer Nullstellen.
mit Hilfe ihrer Nullstellen.
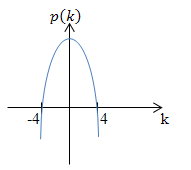
Um jeweils die quadratischen Ungleichungen 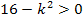 (bzw.
(bzw.  ) zu lösen, muss man jetzt nur noch aus der Skizze ablesen, für welche Werte von k die Parabel
) zu lösen, muss man jetzt nur noch aus der Skizze ablesen, für welche Werte von k die Parabel 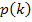 oberhalb (bzw. unterhalb) der k-Achse liegt. Denn
oberhalb (bzw. unterhalb) der k-Achse liegt. Denn 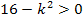 bedeutet nichts anderes als
bedeutet nichts anderes als 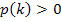 , und das bedeutet wiederum nichts anderes als, dass die y-Werte von
, und das bedeutet wiederum nichts anderes als, dass die y-Werte von 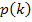 positiv sein sollen, also dass die Hilfsparabel
positiv sein sollen, also dass die Hilfsparabel 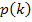 oberhalb der k-Achse liegen soll. Entsprechend ist
oberhalb der k-Achse liegen soll. Entsprechend ist 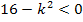 nichts anderes als
nichts anderes als 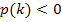 , also muss die Hilfsparabel dann unterhalb der k-Achse liegen. Wir lesen nun einfach aus der Skizze jeweils die entsprechenden Werte von k ab:
, also muss die Hilfsparabel dann unterhalb der k-Achse liegen. Wir lesen nun einfach aus der Skizze jeweils die entsprechenden Werte von k ab:
Zum 2. Fall:
D 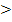 0
0 
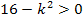
 Parabel
Parabel 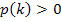 (also
(also 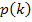 oberhalb der k-Achse) für
oberhalb der k-Achse) für 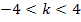 oder in Intervallschreibweise k
oder in Intervallschreibweise k 
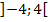
Wenn k Werte aus diesem Bereich annimmt, hat die Gleichung 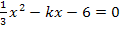 zwei Lösungen.
zwei Lösungen.
Zum 3. Fall:
D 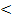 0
0 
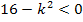
 Parabel
Parabel 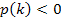 (also
(also 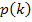 unterhalb der k-Achse) für
unterhalb der k-Achse) für 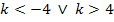 oder in Intervallschreibweise k
oder in Intervallschreibweise k 
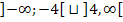
Nimmt k Werte aus diesem Bereich an, hat die Gleichung 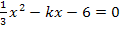 wegen D
wegen D 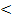 0 keine Lösungen.
0 keine Lösungen.

