Diskriminante D
Es gilt somit:D 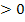 für k
für k  ℝ
ℝ
Die Gleichung hat für beliebige reelle Werte von k zwei verschiedene Lösungen. Eine Fallunterscheidung ist hier erfreulicherweise nicht nötig.
zu c.)
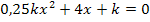
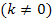
Wichtig ist hierbei die Angabe 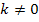 . Da k nicht gleich Null sein kann, ist die gegebene Gleichung immer gemischtquadratisch. Wäre k gleich Null zugelassen gewesen, hätten wir bedenken müssen, dass sich für k = 0 eine lineare Gleichung (Gleichung ohne Quadrat) ergeben hätte und auf diese Gleichung lässt sich die Mitternachtsformel gar nicht anwenden! Das liegt daran, dass hier der Parameter k in der Gleichung auch vor
. Da k nicht gleich Null sein kann, ist die gegebene Gleichung immer gemischtquadratisch. Wäre k gleich Null zugelassen gewesen, hätten wir bedenken müssen, dass sich für k = 0 eine lineare Gleichung (Gleichung ohne Quadrat) ergeben hätte und auf diese Gleichung lässt sich die Mitternachtsformel gar nicht anwenden! Das liegt daran, dass hier der Parameter k in der Gleichung auch vor 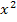 steht. Für k = 0 würde
steht. Für k = 0 würde 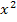 wegfallen und die Gleichung wäre nicht mehr quadratisch. Hätte die Angabe
wegfallen und die Gleichung wäre nicht mehr quadratisch. Hätte die Angabe 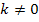 gefehlt, hätten wir den Fall k = 0 gesondert untersuchen müssen:Die für k = 0 entstehende lineare Gleichung
gefehlt, hätten wir den Fall k = 0 gesondert untersuchen müssen:Die für k = 0 entstehende lineare Gleichung 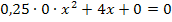 , also
, also 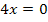 hätte genau eine Lösung, nämlich x = 0.
hätte genau eine Lösung, nämlich x = 0.
Es gilt hier jedoch erfreulicherweise 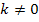 und wir können deshalb, wie bei den vorherigen Beispielen, die Anzahl der Lösungen einfach mit der Diskriminante ermitteln. Wir berechnen wieder zuerst einmal die Diskriminante D.
und wir können deshalb, wie bei den vorherigen Beispielen, die Anzahl der Lösungen einfach mit der Diskriminante ermitteln. Wir berechnen wieder zuerst einmal die Diskriminante D.
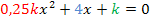
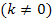
![]()
D = 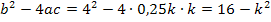
So, hier wird es deutlich komplizierter. Die Diskriminante ist vom Parameter k abhängig und auch das Vorzeichen hängt von k ab, denn im Unterschied zur Teilaufgabe b.) kann hier die Diskriminante sowohl positiv, als auch negativ oder gleich Null werden. In diesem Fall liegt nämlich eine Differenz vor. Das Vorzeichen von D hängt also davon ab, ob 16 gleich, größer oder kleiner als 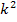 ist. Das Problem ist dabei jedoch, dass wir nun neben einer quadratischen Gleichung auch quadratische Ungleichungen zu lösen haben. Das ist erheblich aufwendiger als das Lösen einer nichtquadratischen Ungleichung.
ist. Das Problem ist dabei jedoch, dass wir nun neben einer quadratischen Gleichung auch quadratische Ungleichungen zu lösen haben. Das ist erheblich aufwendiger als das Lösen einer nichtquadratischen Ungleichung.
Wir beginnen unsere Fallunterscheidung mit dem einfachsten Fall, also D = 0. Dabei ergibt sich eine reinquadratische Gleichung, die leicht zu lösen ist.
1. Fall:
D = 0 
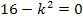 |
| 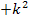
![]()
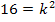 |
| 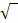
![]()
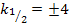
Für 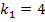 und für
und für 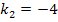 hat die Gleichung
hat die Gleichung 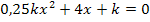
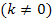 jeweils genau eine Lösung.
jeweils genau eine Lösung.
Weiter geht es mit den heikleren anderen beiden Fällen. Für welche Werte von k wird D nun positiv bzw. negativ? Es ergeben sich die folgenden quadratischen Ungleichungen:
2. Fall:![]() 3. Fall:
3. Fall:
D 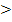 0
0 
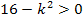
![]() D
D 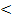 0
0 
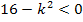
Wir lösen diese beiden quadratischen Ungleichungen praktisch in einem Aufwasch. Dazu verwenden wir ein graphisches Lösungsverfahren. Jeweils die linke Seite der Ungleichungen ist ja identisch;wir stellen uns dazu die Hilfsparabel 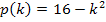 vor. Man kann sie natürlich auch als
vor. Man kann sie natürlich auch als 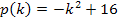 schreiben.
schreiben.

