Diskriminante D
zu a.)
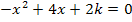
a b c
D 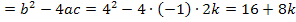
Die Diskriminante D enthält noch den Parameter k. Man sagt, dass D abhängig ist von k. Obwohl hier nur positive Vorzeichen bei D vorkommen, darf man nun nicht glauben, dass D immer positiv ist. Das Vorzeichen von D hängt hier noch von k ab! Wenn du beispielsweise für k den Wert -4 in D einsetzen würdest, käme 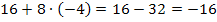 also etwas Negatives heraus! Es stellt sich also die Frage, für welche Werte von k wird D positiv, negativ bzw. gleich Null? Dies bezeichnet man als Fallunterscheidung.
also etwas Negatives heraus! Es stellt sich also die Frage, für welche Werte von k wird D positiv, negativ bzw. gleich Null? Dies bezeichnet man als Fallunterscheidung.
Wir beginnen mit dem Fall D = 0, weil dies eine Gleichung und keine Ungleichung ergibt. Das ist also am einfachsten zu lösen. Für welche Werte von k gilt nun D = 0?
1. Fall:
D = 0 
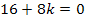 |
| 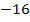
![]()
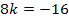 |
| 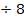
![]()
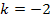
Nun wissen wir, dass für 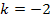 die Diskriminante D = 0 ergibt und somit die gemischtquadratische Gleichung genau eine Lösung hat.
die Diskriminante D = 0 ergibt und somit die gemischtquadratische Gleichung genau eine Lösung hat.
Nun zum zweiten Fall. Für welche Werte von k wird die Diskriminante positiv?
2. Fall:
D 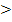 0
0 
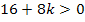 |
| 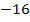
![]()
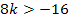 |
| 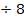
![]()
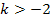
Nun wissen wir, dass für 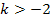 die Diskriminante D
die Diskriminante D 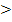 0 wird und somit die gemischtquadratische Gleichung zwei Lösungen hat.
0 wird und somit die gemischtquadratische Gleichung zwei Lösungen hat.
Nun noch der letzte Fall. (Der ist zwar eigentlich schon klar, doch wir rechnen noch einmal alles vor.) Für welche Werte von k wird die Diskriminante negativ?
3. Fall:
D 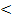 0
0 
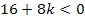 |
| 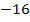
![]()
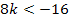 |
| 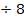
![]()
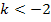
Nun wissen wir, dass für 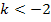 die Diskriminante D
die Diskriminante D 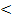 0 ist und somit die gemischtquadratische Gleichung keine Lösung hat.
0 ist und somit die gemischtquadratische Gleichung keine Lösung hat.
Hier noch einmal alles zusammengefasst:
Für 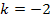 : D = 0
: D = 0  Genau 1 Lösung
Genau 1 Lösung
Für 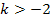 : D
: D 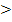 0
0  2 verschiedene Lösungen
2 verschiedene Lösungen
Für 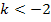 : D
: D 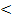 0
0  Keine Lösung
Keine Lösung
zu b.)
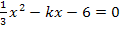
Bei dieser Gleichung multiplizieren wir erst einmal mit dem Faktor 3, damit wir nicht mit Brüchen weiterrechnen müssen. Das muss man zwar nicht unbedingt machen, es erleichtert die weitere Rechnung jedoch erheblich. Wer rechnet schon gerne mit Brüchen, wenn es nicht unbedingt sein muss? Also multipliziert man besser mit dem Hauptnenner, in diesem Fall eben mit dem Faktor 3. Die rechte Seite ändert sich dadurch nicht, denn 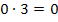 . Nur auf der linken Seite muss alles mit 3 multipliziert werden.
. Nur auf der linken Seite muss alles mit 3 multipliziert werden.
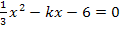 |
| 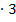
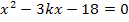
Jetzt kann die Diskriminante leichter berechnet werden.
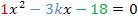
![]()
D = 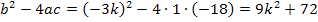
Hier können wir sofort erkennen, dass die Diskriminante zwar von k abhängig ist, dass jedoch das Vorzeichen von D immer positiv ist, egal, was für k eingesetzt wird. Das liegt daran, dass wegen der geraden Potenz der Ausdruck 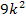 nicht negativ werden kann. Addiert man auch noch 72 zu
nicht negativ werden kann. Addiert man auch noch 72 zu 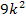 kann nur noch etwas Positives herauskommen.
kann nur noch etwas Positives herauskommen.

