Diskriminante D
a.)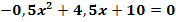 
b.)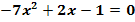 
c.)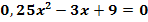 
Lösung:
Die Lösungen sollen laut Angabe nicht „explizit“ ermittelt werden. Hä? Was soll denn das wieder heißen? Keine Sorge, das bedeutet bloß, dass die Lösungen nicht wirklich ausgerechnet werden sollen. In der Aufgabenstellung ist also verlangt, nur die Anzahl der Lösungen, jedoch nicht die Lösungen der gemischtquadratischen Gleichungen selbst zu ermitteln. Daher müssen wir die Diskriminante D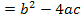 
berechnen. Ist D positiv hat die Gleichung zwei Lösungen. Ist D negativ, gibt es keine Lösung. Ist D gleich Null, gibt es genau eine Lösung.
Alle drei Gleichungen sind schon nach Null aufgelöst, sie liegen also bereits in der Form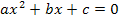 
vor. Wir können also direkt erkennen, was jeweils a, b und c ist. Die Diskriminante lässt sich deshalb ganz leicht berechnen. Also los! Versuch es doch gleich ´mal alleine! Zur Kontrolle findest du natürlich im Folgenden die ausführlichen Lösungen.
zu a.)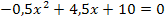 
a b c
D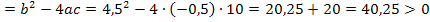 
2 Lösungen
zu b.)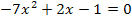 
a b c
D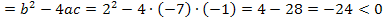 
Keine Lösung
zu c.)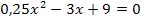 
a b c
D 
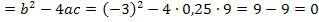
1 Lösung
Das war doch wirklich nicht schwer, oder? Du ahnst es aber wahrscheinlich schon:Es bleibt nicht so einfach. Deutlich anspruchsvoller sind Aufgaben, die neben der Unbekannten x noch einen weiteren Buchstaben, einen sogenannten Parameter enthalten. Die Anzahl der Lösungen kann dabei nämlich vom Parameter abhängen. Man muss dann eine Fallunterscheidung durchführen und Fallunterscheidungen mögen die wenigsten Schüler. Ich kenne überhaupt keinen, der sie mag. Im Gegenteil:Fallunterscheidungen sind eigentlich allen ein Graus! Doch so schlimm sind die Fallunterscheidungen auch wieder nicht. Wenn man weiß, wie etwas geht, ist es gleich nicht mehr so schlimm. Also schauen wir uns doch ein paar Beispiele dafür an. An Hand dieser Beispiele soll das Grundprinzip einer Fallunterscheidung erklärt werden. Schaue dir wirklich jede der Teilaufgaben genau an! Sie sehen zwar am Anfang alle sehr ähnlich aus, doch ergeben sich im 2. Bsp. bei den drei Teilaufgaben a.) bis c.) letztendlich drei völlig andere Rechnungen.
2. Bsp.:
Ermittle die Anzahl der Lösungen der folgenden Gleichungen in Abhängigkeit vom Parameter k!
a.)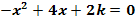 
b.)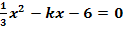 
c.)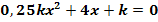 
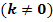
Lösung:
Bei jeder der drei Teilaufgaben handelt es sich um eine gemischtquadratische Gleichung. Sie liegt jeweils in der von uns benötigten Form 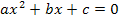vor. Wir können also direkt erkennen, was jeweils a, b und c ist. Die Diskriminante lässt sich deshalb sofort berechnen. Du musst dir dabei jedoch den Parameter k als konkrete, obwohl unbekannte Zahl vorstellen. Unterscheide also genau zwischen Variable x und Parameter k. Also los! Versuch es doch gleich ´mal alleine jeweils die Diskriminante zu berechnen! Zur Kontrolle findest du natürlich im Folgenden die ausführlichen Lösungen. Ob dann eine Fallunterscheidung nötig ist, hängt davon ab, ob der für D ermittelte Ausdruck noch k enthält und wenn ja, ob das Vorzeichen dieses Ausdrucks vom Parameter abhängt.
