Die Mitternachtsformel

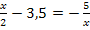
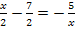
„Kreuzweise Multiplizieren“

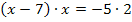
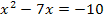
Jetzt erkennst du bestimmt, dass es sich bei dieser Gleichung wieder um eine gemischtquadratische Gleichung handelt, da schließlich 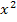und x in der Gleichung vorkommen. Wir bringen sie erst auf die Form 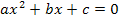, d.h. wir bringen die -10 auf die linke Seite, damit auf der rechten Seite nur noch die Zahl Null steht.

|

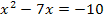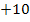
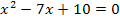
Nun verwenden wir wieder die Mitternachtsformel, um nach x aufzulösen. Was hier a, b und c ist, dürftest du inzwischen leicht erkennen:

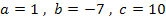
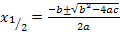
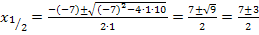
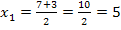
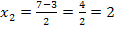
Die soeben berechneten x-Werte liegen innerhalb der Definitionsmenge, daher lautet die Lösungsmenge:L =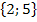

Die folgenden beiden Beispiele zeigen Aufgaben die mit Hilfe einer Substitution gelöst werden.

---