Die Mitternachtsformel
Die Definitionsmenge enthält, wie du sicher weißt, alle Zahlen der Grundmenge G, die für x eingesetzt werden dürfen. Da in der Aufgabenstellung keine Angabe über die Grundmenge G gemacht wurde, gehst du einfach von der größten dir bekannten Menge, also der Menge der reellen Zahlen ℝaus. Da die Division durch Null nicht definiert ist, darf der Nenner der Bruchgleichung nicht gleich Null werden. Daher darf hier für x nicht Null eingesetzt werden, da sich sonst bei dem Bruch 
im Nenner Null ergeben würde. Bei x = 0 liegt also eine Definitionslücke vor. Alle anderen reellen Zahlen dürfen hier für x eingesetzt werden. Die Definitionsmenge D lautet daher:
D = ℝ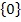 
Das war nicht schwer, doch nun müssen wir uns der Berechnung der Lösungsmenge widmen. Erst ab jetzt wird es interessant, d.h. nicht mehr ganz so leicht. Wie löst man denn eigentlich eine Gleichung, die im Nenner x enthält? Wie immer gibt es dafür verschiedene Methoden. Sie werden ausführlich im Kapitel Bruchgleichungen erläutert. Hier eine Methode ganz kurz gesagt:Man bringt sowohl die linke als auch die rechte Seite der Gleichung jeweils auf einen gemeinsamen Nenner;die rechte Seite unserer Gleichung besteht sowieso nur aus einem Bruch, daher entfällt hier auf der rechten Seite dieser Schritt. Danach multipliziert man „kreuzweise“, d.h. man multipliziert den ganzen Zähler der linken Seite mit dem Nenner der rechten Seite und umgekehrt den Zähler der rechten Seite mit dem Nenner der linken. Vergleiche unten! Am besten verstehst du das sicherlich, wenn du dir die nächsten Schritte genau anschaust. Da wird es vorgemacht, wie es geht.
