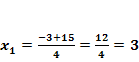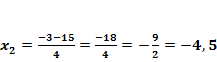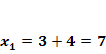Die Mitternachtsformel
Wir brauchen also die Mitternachtsformel, um sie zu lösen. Da die Gleichung bereits nach Null aufgelöst ist, kannst du sofort erkennen, was in dieser Gleichung den Koeffizienten a, b und c entspricht:
a = 2, b = 3, c = -27
Einsetzen in die Mitternachtsformel 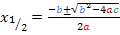 ergibt:
ergibt:
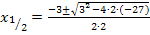
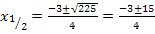
Jetzt haben wir die x-Koordinaten der Nullstellen berechnet;wir müssen die Nullstellen nur noch als Punkte angeben. Die y-Koordinate ist dabei natürlich jeweils y = 0.
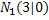
![]()
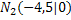
Weitere Aufgabenbeispiele und ausführlichere Erklärungen zur Nullstellenberechnung von Parabeln findest du im Kapitel Nullstellen einer quadratischen Funktion.
7. Bsp.:
Berechne die Schnittpunkte der Parabel p:y = 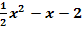 mit der Gerade g:y =
mit der Gerade g:y = 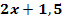 !
!
Lösung:
Um die Schnittpunkte zweier Funktionen zu berechnen, setzt man die Funktionen gleich und löst nach x auf. Da hier durch das Gleichsetzen von p und g eine gemischtquadratische Gleichung entsteht, müssen wir erst nach Null auflösen, damit wir danach die Mitternachtsformel anwenden können.
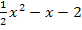 =
= 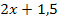 |
| 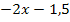
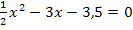
Wir überlegen uns wieder, was a, b und c entspricht:
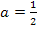 ,
, 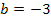 ,
, 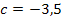
Einsetzen in die Mitternachtsformel 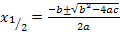 ergibt:
ergibt:
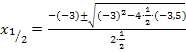
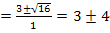
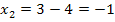
Nun haben wir die x-Koordinaten der beiden Schnittpunkte berechnet. Es fehlen also nur noch die jeweiligen y-Koordinaten. Wir erhalten sie, indem wir die soeben berechneten x-Koordinaten jeweils in eine der beiden Funktionen p oder g einsetzen. In welche man einsetzt, ist egal, den die Schnittpunkte liegen schließlich sowohl auf p als auch auf g. Da die Gleichung von g einfacher ist, setzen wir in g:y = 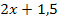 ein. Das ergibt:
ein. Das ergibt:
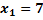 in g:
in g:![]()
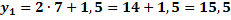
![]()

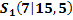
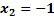 in g:
in g:![]()
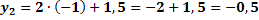

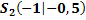
Damit ist die Aufgabe gelöst. Sollen die Schnittpunkte zweier Parabeln berechnet werden, geht man prinzipiell genauso vor. Konkrete Beispiele dazu findest du Kapitel Lagebeziehungen zwischen zwei Parabeln. Ausführlichere Erklärungen und weitere Beispiele und zur Berechnung von Schnittpunkten einer Parabel und einer Gerade sind im Kapitel Lagebeziehungen zwischen Parabel und Gerade dargestellt.
Nun schauen wir uns als nächstes ein Beispiel für eine Bruchgleichung an, die letztendlich zu eine gemischtquadratischen Gleichung der Form 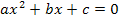 führt und somit wieder mit der Mitternachtsformel gelöst werden kann.
führt und somit wieder mit der Mitternachtsformel gelöst werden kann.
8. Bsp.:
Gib die Definitions- und Lösungsmenge der Gleichung 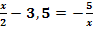 an!
an!
Lösung:
Die Definitionsmenge kann man sich hier ganz leicht überlegen.