Die Mitternachtsformel
Dann gibt es einfach keine Lösung. Mehr über den Zusammenhang zwischen Diskriminante und Anzahl der Lösungen der Gleichung 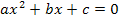 findest du im Kapitel Diskriminante D.
findest du im Kapitel Diskriminante D.
Bevor wir uns weitere Beispiele anschauen, fassen wir noch einmal alles Wichtige zu diesem Typ stichpunktartig zusammen.
| Anleitung zum Lösen gemischtquadratischer Gleichungen:
· Gleichung nach Null auflösen (falls nötig) · Überlegen, was in deiner Aufgabe a, b und c entspricht · Einsetzen in die Mitternachtsformel · · Fertig! |
Wenn du dich fragst, wofür du das in der Mathematik überhaupt brauchst, schau´dir einfach die nächsten Beispiele an! Dort siehst du viele verschiedene Aufgabenstellungen, z.B. die Nullstellenberechnung einer Parabel oder die Schnittpunktberechnung einer Parabel mit einer Geraden oder einer zweiten Parabel, die alle letztendlich zu einer gemischtquadratischen Gleichung führen, die man dann mit dem gerade gezeigten Verfahren löst. Oft ist zu Beginn einer Aufgabe noch gar nicht ersichtlich, dass man am Schluss die Mitternachtsformel braucht. So kann beispielsweise eine Bruchgleichung (d.h. eine Gleichung mit x im Nenner) zu einer gemischtquadratischen Gleichung führen. Auch manche zuerst kompliziert wirkende Gleichungen lassen sich durch eine geeignete Substitution (vom lateinischen substituere = ersetzen) in eine Gleichung der Form 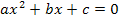 umwandeln, die dann bequem mit der Mitternachtsformel gelöst werden kann. Wie das Prinzip der Substitution genau funktioniert, wird im 9. und 10. Bsp. vorgeführt. Als nächstes soll jedoch erst eine einfachere Aufgabe vorgeführt werden.
umwandeln, die dann bequem mit der Mitternachtsformel gelöst werden kann. Wie das Prinzip der Substitution genau funktioniert, wird im 9. und 10. Bsp. vorgeführt. Als nächstes soll jedoch erst eine einfachere Aufgabe vorgeführt werden.
6. Bsp.:
Berechne die Nullstellen der Funktion f:y = 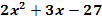 !
!
Lösung:
Wie du sicher weißt, handelt es sich bei den Nullstellen einer Funktion um die Schnittpunkte des Graphen mit der x-Achse. Sie werden berechnet, indem die Funktion gleich Null gesetzt wird, da ja jeder Punkt, der auf der x-Achse liegt, den y-Wert y = 0 haben muss. (Wäre y positiv, würde der Punkt oberhalb der x-Achse liegen;wäre y negativ unterhalb.) Ob man nun für y Null einsetzt oder die Funktion gleich Null setzt, ist natürlich das Selbe. Also setzen wir unsere Funktion f erst ´mal gleich Null:
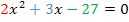
Das ist eine Gleichung vom Typ 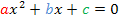 .
.


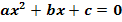
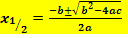
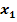 und
und 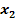 ausrechnen (falls der Ausdruck unter der Wurzel nicht negativ ist)
ausrechnen (falls der Ausdruck unter der Wurzel nicht negativ ist)