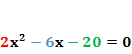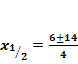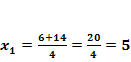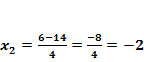Die Mitternachtsformel
Sie liegt ja schon so vor, wie wir sie brauchen, also in der Form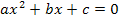 
. Du darfst dann allerdings nicht auf die Idee kommen, die Konstante, hier die Zahl -20, wieder auf die andere Seite zu bringen. (Das ist zwar nicht falsch, hilft uns aber nicht weiter.) Wir wollen schließlich die Mitternachtsformel verwenden, um die gemischtquadratische Gleichung nach x aufzulösen, und dazu müssen wir uns zuerst überlegen, was in unserer Gleichung den Koeffizienten a, b und c entspricht. Das kann man jedoch nur dann gut erkennen, wenn die Gleichung nach Null aufgelöst ist. Vergleiche jetzt die allgemeine Form der gemischtquadratischen Gleichung 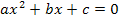mit der Gleichung unseres Beispiels und überlege dir, was denn hier a, b bzw. c ist:
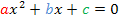
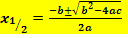(Mitternachtsformel)
a steht immer für die Zahl vor dem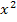 
, b entsprechend für die Zahl vor dem x und c für die Zahl ohne x. Damit es dir leichter fällt zu erkennen, was hier a, b und c ist, wurde a in Rot, b in Blau und c in Grün geschrieben. Somit müsstest du nun ablesen können:
In diesem Beispiel gilt: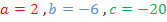 
Achte dabei auch besonders auf die Vorzeichen! Gerade vergessene Minuszeichen gehören zu den häufigsten Fehlerquellen bei der Verwendung der Mitternachtsformel! Du musst also die entsprechenden Vorzeichen „mitnehmen“. Auch wenn im allgemeinen Ansatz der gemischtquadratischen Gleichung 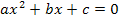ein Plus-Zeichen vor b und c steht, heißt das noch lange nicht, dass b und c jeweils positiv sein müssen! Das siehst du ja schon an diesem Beispiel. Hier ist b = -6 und nicht +6. Das Gleiche gilt in diesem Beispiel für c. Es gilt nämlich c = -20 und nicht +20. a ist hier zwar positiv, aber das ist nicht bei allen Aufgaben so. In anderen Aufgaben kann auch a negativ sein.
Jetzt müssen wir nur noch für a, b und c die entsprechenden Werte in die Mitternachtsformel einsetzen und den entstandenen Term ausrechnen. Mit 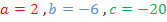erhält man:
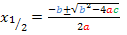(Mitternachtsformel)
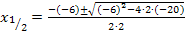Beachte beim Ausrechnen die Regel:Punkt vor Strich!
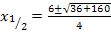
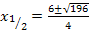
Erst ab jetzt rechnen wir getrennt mit Plus bzw. Minus im Zähler weiter und erhalten so die zwei Lösungen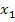 
und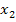 
.
Nun denkst du dir vielleicht:Puh! Was für eine lange Rechnung! Ok, hier sieht das wohl wirklich so aus. Das liegt aber nur daran, dass auch wirklich jeder noch so kleine Zwischenschritt gezeigt wurde, damit du den Rechenweg gut nachvollziehen kannst. Du musst allerdings nicht alle Zwischenschritte hinschreiben, wenn du selber rechnest. Dann wird es gleich viel kürzer. Du kannst ja auch den Taschenrechner zu Hilfe nehmen.
