Die Mitternachtsformel
Die Schreibweise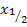 
bedeutet übrigens nicht etwa 
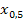, sondern ist nur eine abgekürzte Schreibweise für die beiden Lösungen 
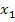und 
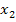. (Falls du das Kapitel Quadratwurzel auf dieser website schon gelesen hast, kennst du diese Schreibweise bereits von da, denn dort wird diese Schreibweise ebenfalls verwendet. Im Typ I taucht sie am Ende des 1. Bsp. auch schon auf.) Die beiden verschiedenen Lösungen ergeben sich, da man im Zähler am Ende der Rechnung einmal mit Plus vor der Wurzel und einmal mit Minus davor rechnen muss.
Bei der Behandlung der gemischtquadratischen Gleichungen in der Schule wird (leider) fast immer zuerst der kompliziertere Lösungsweg durch quadratische Ergänzung gezeigt, weil sich damit die einfachere Mitternachtsformel herleiten lässt. Zuerst kommt in der Schule also ein echt ziemlich schwieriges Verfahren und erst viel später der einfachere Weg. Viele Schüler müssen daher wohl denken:Warum einfach, wenn es auch kompliziert geht!?! Weil du wahrscheinlich nur wissen willst, wie man gemischtquadratische Gleichungen am einfachsten löst, soll hier entgegen der Regel als erstes gezeigt werden, wie sich gemischtquadratische Gleichungen mit der Mitternachtsformel lösen lassen. Wenn es dich aber doch interessiert, wie die Mitternachtsformel hergeleitet wird, musst du zuerst die quadratische Ergänzung lernen. Von der Quadratischen Ergänzung (zur Lösung gemischtquadratischer Gleichungen)kommst du dann zur Herleitung der Mitternachtsformel.
Jetzt möchtest du sicher endlich wissen, wie man denn nun solche Gleichungen rechnerisch lösen kann. Also schauen wir uns ´mal ein konkretes Beispiel an.
5. Bsp.: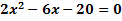 
Ermittle rechnerisch die Lösungsmenge dieser Gleichung!
Lösung:
Die Gleichung ist gemischtquadratisch und enthält auch eine Konstante (d.h. eine Zahl ohne x, in diesem Beispiel -20). Wegen der Konstanten -20 lässt sich x nicht einfach ausklammern. Deshalb kann die Methode, die wir in den Beispielen 3 und 4 verwendet haben, nicht benützt werden. Zur Lösung dieser Gleichung brauchen wir die bereits oben erwähnte Mitternachtsformel. Sie kann jedoch nur dann angewendet werden, wenn die Gleichung in der Form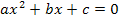 
vorliegt, also wenn sie nach Null aufgelöst ist. Das ist in diesem Beispiel bereits der Fall. (Wäre das nicht so, müssten wir sie selbst erst auf diese Form bringen.)
Merke:Alle gemischtquadratischen Gleichungen, also Gleichungen mit 
und x, müssen zuerst nach Null aufgelöst werden, damit man sie mit der Mitternachtsformel lösen kann. Bringe deshalb alles auf eine Seite der Gleichung, so dass … = 0 dasteht!
Wenn die Gleichung, wie auch in diesem Beispiel, bereits in dieser Form vorliegt, ist das natürlich nicht mehr nötig.
