Lösungsweg 2 zu Bsp. 5b (mit zwei Gleichungen für zwei Unbekannte)

Hier noch einmal die Angabe:

Die Einer-Ziffer einer zweistelligen Zahl ist um 1 kleiner als die Zehner-Ziffer dieser Zahl. Multipliziert man diese Zahl mit ihrer Spiegelzahl ergibt sich 736. Was war die ursprüngliche Zahl? (Die Spiegelzahl erhält man durch Vertauschen der Einer- und Zehner-Ziffer.)

Wir bezeichnen die Zehnerziffer der ursprünglichen Zahl mit x und die Einer-Ziffer dieser Zahl mit y.

Ursprüngliche Zahl:

Zehner-Ziffer: x

Einer-Ziffer: y

Laut Angabe ist die Einer-Ziffer y um 1 kleiner als die Zehner-Ziffer x der gesuchten Zahl. Man muss daher zu der kleineren Einer-Ziffer y genau 1 dazuzählen, um die größere Zehner-Ziffer y zu erhalten. So erhalten wir die folgende Gleichung:

I          y + 1 = x

Hinweis:Man hätte natürlich auch sagen können, dass man von der größeren Zehner-Ziffer x die Zahl 1 abziehen muss, um die kleinere Einer-Ziffer y zu erhalten. So käme man zu der Gleichung x – 1 = y. Diese Gleichung ist äquivalent zur Gleichung I, da sie sich durch einfache Umformung ineinander überführen lassen.

Eine Gleichung mit x und y haben wir nun vorliegen;wir brauchen aber noch eine zweite. Diese Gleichung zu finden wird deutlich anspruchsvoller. Erinnern wir uns noch einmal an die Angabe:Dort steht sinngemäß, dass das Produkt der gesuchten Zahl mit ihrer Spiegelzahl 736 ergibt. Wir müssen daher das Produkt der Zahl mit ihrer Spiegelzahl durch x und y ausdrücken. Damit du den Überblick nicht verlierst, gehen wir dabei schrittweise vor.

Ursprüngliche Zahl: Spiegelzahl:

Zehner-Ziffer: x Zehner-Ziffer: y

Einer-Ziffer: y Einer-Ziffer: x

Zahl (insgesamt):        10x + y Spiegelzahl (insgesamt):         10y + x

Die Zahl (insgesamt) und die Spiegelzahl (insgesamt) haben wir gebildet, indem wir die Zehner-Ziffer mit ihrem Wert 10 multipliziert und mit der Einer-Ziffer addiert haben. Warum das so funktioniert, wurde schon beim ersten Lösungsweg erklärt. Sollte dir dieser Schritt nicht klar sein, lies noch einmal ganz genau die Erklärungen beim ersten Lösungsweg dieser Teilaufgabe!

Jetzt multiplizieren wir einfach die ursprüngliche Zahl (insgesamt) mit ihrer Spiegelzahl (insgesamt) und setzen das Ganze gleich 736. So erhalten wir die zweite benötigte Gleichung mit x und y.

II         

Wir schreiben uns noch einmal beide Gleichungen übersichtlich direkt unter einander.

I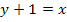         

II         

Es liegt nun ein Gleichungssystem bestehend aus zwei Gleichungen für zwei Unbekannte vor. Eigentlich würde es sich hier anbieten, die Gleichung I direkt für x in die Gleichung II einzusetzen, weil Gleichung I bereits nach x aufgelöst dasteht. Dann würde allerdings die Unbekannte y in der Gleichung verbleiben und x herausfallen. Man könnte dann y berechnen und letztendlich auch x, indem man den für y berechneten Wert in Gleichung I einsetzt. Da wir hier jedoch wieder auf die selbe Gleichung wie schon beim ersten Lösungsweg kommen wollen, lösen wir die Gleichung I zuerst nach y auf und setzen das in Gleichung II für y ein. Dadurch fällt nämlich die Unbekannte y heraus und wir kommen nach Vereinfachen zu genau der selben Gleichung, die wir schon beim ersten Lösungsweg aufgestellt hatten.

I          |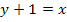

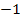
I´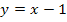         

I´in II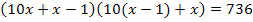

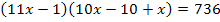
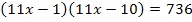
Ab jetzt geht es im Prinzip wieder genauso weiter wie beim ersten Lösungsverfahren. Man löst die Gleichung nach x auf. Das Ergebnis x = 3 (vergleiche erster Lösungsweg) setzt man dann in I´ein und erhält so:

y = 3 – 1 = 2

Dass die ursprüngliche Zahl 32 ist, haben wir ja bereits beim ersten Lösungsweg festgestellt.